题目内容
已知椭圆C:
+
=1(a>0,b>0),右焦点为F(
,0),且点B(0,1)在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知A1,A2分别是椭圆C的左,右顶点,M是第一象限内椭圆上一点,直线MA2,MA1分别与y轴交于P,Q两点,PB=2BQ,求M点的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(1)求椭圆C的标准方程;
(2)已知A1,A2分别是椭圆C的左,右顶点,M是第一象限内椭圆上一点,直线MA2,MA1分别与y轴交于P,Q两点,PB=2BQ,求M点的坐标.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)根据椭圆的几何性质求解c=
,b=1,a=2,可得方程,(2)设M点的坐标为(x0,y0),根据题意得出
+y02=1,x0>0,y0>0,1-
=2(
-1)
即3x
+12y0-2x0y0=12,联立方程组求解即可.
| 3 |
| x02 |
| 4 |
| 2y0 |
| 2-x0 |
| 2y0 |
| x0+2 |
即3x
2 0 |
解答:
解:(1)∵椭圆C:
+
=1(a>0,b>0),右焦点为F(
,0),且点B(0,1)在椭圆C上,
∴c=
,b=1,a=2,
∴椭圆C的标准方程为:
+y2=1,
(2)∵A1,A2分别是椭圆C的左,右顶点,
∴A1(-2,0),A2(2,0),B(0,1)
设M点的坐标为(x0,y0).
∵M是第一象限内椭圆上一点,直线MA2,MA1分别与y轴交于P,Q两点,PB=2BQ,
∴
+y02=1,x0>0,y0>0,①
yp=
,yQ=
,
∵PB=2BQ,
∴1-
=2(
-1)
即3x
+12y0-2x0y0=12,②
有①②解得:x0=6-6y0,③
6-6y0>0,y0<1
把③代入①得:5y
-9y0+4=0,
即:y0=1(舍去),y0=
,
把y0=
,代入③得;x0=
,
∴M点的坐标(
,
)
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
∴c=
| 3 |
∴椭圆C的标准方程为:
| x2 |
| 4 |
(2)∵A1,A2分别是椭圆C的左,右顶点,
∴A1(-2,0),A2(2,0),B(0,1)
设M点的坐标为(x0,y0).
∵M是第一象限内椭圆上一点,直线MA2,MA1分别与y轴交于P,Q两点,PB=2BQ,
∴
| x02 |
| 4 |
yp=
| 2y0 |
| 2-x0 |
| 2y0 |
| x0+2 |
∵PB=2BQ,
∴1-
| 2y0 |
| 2-x0 |
| 2y0 |
| x0+2 |
即3x
2 0 |
有①②解得:x0=6-6y0,③
6-6y0>0,y0<1
把③代入①得:5y
2 0 |
即:y0=1(舍去),y0=
| 4 |
| 5 |
把y0=
| 4 |
| 5 |
| 6 |
| 5 |
∴M点的坐标(
| 6 |
| 5 |
| 4 |
| 5 |
点评:本题考查了椭圆难度性质,方程,直线与椭圆的位置关系,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
函数f(x)=
的定义域为( )
| 1 | ||||
|
A、(0,
| ||
B、(
| ||
C、(0,
| ||
D、(-∞,
|
已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是( )
| A、(0,1) | ||||
B、(0,
| ||||
| C、(-1,0) | ||||
D、(-
|
一条直线与两条异面直线中的一条相交,那么它与另一条直线之间的位置关系是( )
| A、异面 | B、相交或平行或异面 |
| C、相交 | D、平行 |

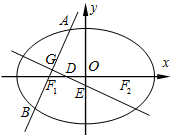 如图,已知椭圆C:
如图,已知椭圆C: