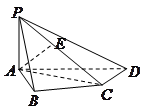题目内容
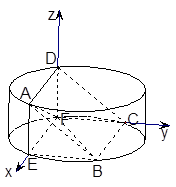
如图,圆柱的高为2,底面半径为3,AE、DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形.
(1)求证: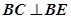 ;
;
(2)求正方形ABCD的边长;
(3)求直线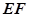 与平面
与平面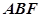 所成角的正弦值.
所成角的正弦值.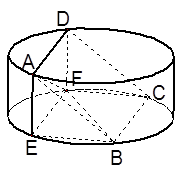
(1)求证:
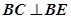 ;
;(2)求正方形ABCD的边长;
(3)求直线
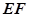 与平面
与平面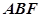 所成角的正弦值.
所成角的正弦值.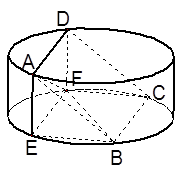
(1) AE是圆柱的母线
AE是圆柱的母线
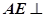 底面BEFC, 又
底面BEFC, 又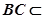 面BEFC
面BEFC 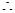
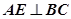
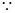 又
又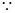 ABCD是正方形
ABCD是正方形 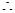
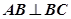 又
又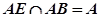
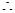
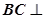 面ABE
面ABE
又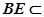 面ABE
面ABE 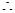
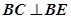 …… 3分
…… 3分
(2)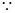 四边形
四边形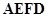 为矩形,且ABCD是正方形
为矩形,且ABCD是正方形 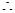 EF
EF BC
BC
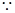
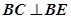
 四边形EFBC为矩形
四边形EFBC为矩形
 BF为圆柱下底面的直径 …… 4分
BF为圆柱下底面的直径 …… 4分
设正方形ABCD的边长为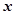 ,则AD=EF=AB=
,则AD=EF=AB=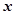
在直角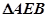 中AE=2,AB=
中AE=2,AB=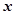 ,且BE2+AE
,且BE2+AE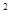 = AB
= AB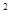 ,得BE
,得BE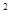 =
=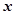 2-4
2-4
在直角 中BF=6,EF=
中BF=6,EF=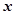 ,且BE
,且BE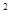 +EF
+EF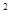 = BF
= BF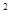 ,的BE2=36-
,的BE2=36-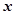 2 …… 6分
2 …… 6分
解得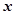 =
=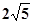 ,即正方形ABCD的边长为
,即正方形ABCD的边长为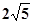 …… 7分
…… 7分
(3)如图以F为原点建立空间直角坐标系,则A(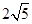 ,0,2),B(
,0,2),B(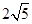 ,4,0),
,4,0),
E(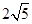 ,0,0),
,0,0),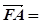 (
(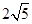 ,0, 2),
,0, 2),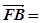 (
(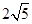 ,4,0),
,4,0), 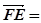 (
(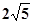 ,0,0)
,0,0)
设面AEF的法向量为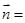 (
(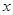 ,
,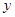 ,
,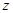 ),则
),则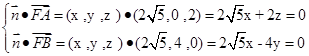
令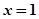 ,则
,则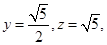 即
即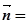 (
(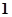 ,
,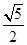 ,-
,-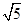 ) …… 11分
) …… 11分
设直线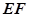 与平面
与平面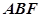 所成角的大小为
所成角的大小为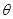 ,则
,则
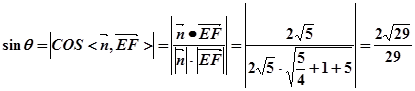 …… 12分
…… 12分
所以直线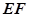 与平面
与平面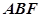 所成角的正弦值为
所成角的正弦值为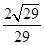 .
.
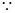 AE是圆柱的母线
AE是圆柱的母线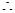
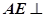 底面BEFC, 又
底面BEFC, 又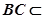 面BEFC
面BEFC 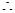
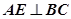
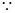 又
又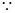 ABCD是正方形
ABCD是正方形 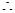
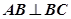 又
又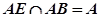
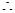
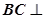 面ABE
面ABE 又
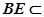 面ABE
面ABE 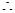
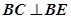 …… 3分
…… 3分(2)
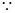 四边形
四边形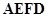 为矩形,且ABCD是正方形
为矩形,且ABCD是正方形 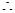 EF
EF BC
BC 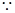
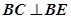
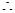 四边形EFBC为矩形
四边形EFBC为矩形  BF为圆柱下底面的直径 …… 4分
BF为圆柱下底面的直径 …… 4分 设正方形ABCD的边长为
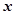 ,则AD=EF=AB=
,则AD=EF=AB=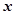
在直角
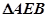 中AE=2,AB=
中AE=2,AB=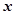 ,且BE2+AE
,且BE2+AE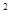 = AB
= AB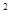 ,得BE
,得BE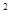 =
=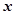 2-4
2-4 在直角
 中BF=6,EF=
中BF=6,EF=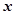 ,且BE
,且BE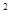 +EF
+EF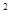 = BF
= BF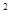 ,的BE2=36-
,的BE2=36-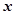 2 …… 6分
2 …… 6分解得
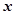 =
=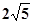 ,即正方形ABCD的边长为
,即正方形ABCD的边长为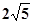 …… 7分
…… 7分(3)如图以F为原点建立空间直角坐标系,则A(
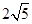 ,0,2),B(
,0,2),B(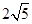 ,4,0),
,4,0),
E(
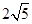 ,0,0),
,0,0),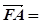 (
(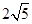 ,0, 2),
,0, 2),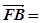 (
(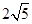 ,4,0),
,4,0), 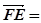 (
(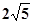 ,0,0)
,0,0) 设面AEF的法向量为
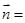 (
(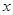 ,
,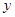 ,
,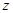 ),则
),则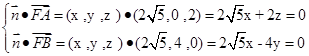
令
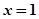 ,则
,则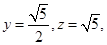 即
即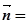 (
(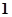 ,
,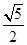 ,-
,-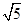 ) …… 11分
) …… 11分设直线
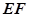 与平面
与平面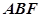 所成角的大小为
所成角的大小为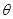 ,则
,则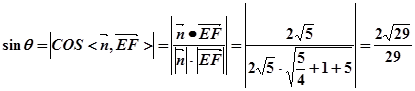 …… 12分
…… 12分所以直线
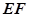 与平面
与平面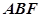 所成角的正弦值为
所成角的正弦值为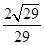 .
.(1)证明线线垂直,可以通过证明线面垂直来解决.本题只要证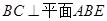 即可.(2)在
即可.(2)在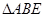 中求AB的长,在
中求AB的长,在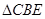 中求BC的长,然后根据AB=BC即可求出BE的长度.进而确定正方形ABCD的边长.
中求BC的长,然后根据AB=BC即可求出BE的长度.进而确定正方形ABCD的边长.
(3)可以借助向量建系来解决,也可以利用三垂线定理作出直线FE与平面ABF所成的角.然后再求解.
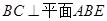 即可.(2)在
即可.(2)在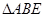 中求AB的长,在
中求AB的长,在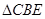 中求BC的长,然后根据AB=BC即可求出BE的长度.进而确定正方形ABCD的边长.
中求BC的长,然后根据AB=BC即可求出BE的长度.进而确定正方形ABCD的边长.(3)可以借助向量建系来解决,也可以利用三垂线定理作出直线FE与平面ABF所成的角.然后再求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
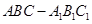 中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。
中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。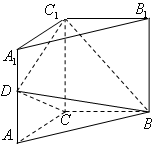
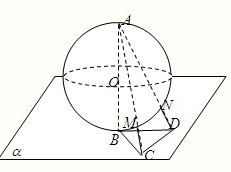
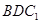 ⊥平面
⊥平面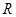 的球
的球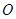 的直径
的直径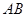 垂直于平面
垂直于平面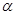 ,垂足为
,垂足为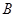 ,
,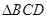 是平面
是平面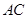 、
、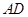 分别与球面交于点M,N,那么M、N两点间的球面距离是( )
分别与球面交于点M,N,那么M、N两点间的球面距离是( )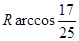
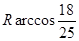
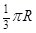
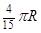
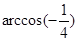
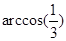
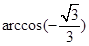
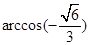
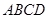 与
与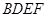 均为菱形,
均为菱形,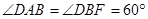 ,且
,且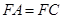 .
.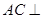 平面
平面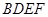 ;
;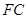 ∥平面
∥平面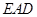 ;
;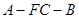 的余弦值.
的余弦值.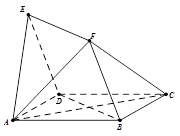
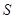 是
是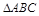 所在平面外的一点,且
所在平面外的一点,且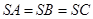 ,若
,若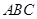 内的射影落在
内的射影落在 ABC外部,则
ABC外部,则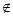 直线l , 则由点P和直线l确定的平面的个数是
直线l , 则由点P和直线l确定的平面的个数是 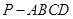 中,
中,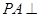 底面
底面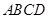 ,
,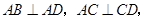
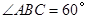 ,
,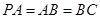 ,
, 是
是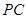 的中点.
的中点.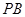 和平面
和平面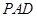 所成的角的大小;
所成的角的大小;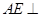 平面
平面 ;
;