题目内容
如图,四边形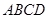 与
与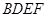 均为菱形,
均为菱形,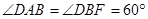 ,且
,且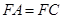 .
.
(Ⅰ)求证: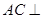 平面
平面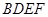 ;
;
(Ⅱ)求证: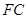 ∥平面
∥平面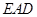 ;
;
(Ⅲ)求二面角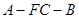 的余弦值.
的余弦值.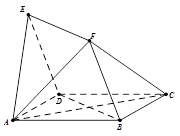
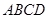 与
与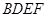 均为菱形,
均为菱形,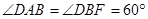 ,且
,且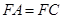 .
.(Ⅰ)求证:
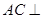 平面
平面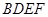 ;
;(Ⅱ)求证:
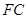 ∥平面
∥平面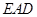 ;
;(Ⅲ)求二面角
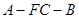 的余弦值.
的余弦值.
(Ⅰ)证明:设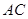 与
与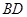 相交于点
相交于点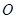 ,连结
,连结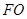 .
.
因为 四边形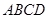 为菱形,所以
为菱形,所以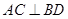 ,
,
且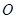 为
为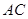 中点. ………………1分
中点. ………………1分
又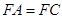 ,所以
,所以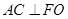 . ………3分
. ………3分
因为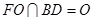 ,
,
所以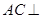 平面
平面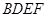 . ………………4分
. ………………4分
(Ⅱ)证明:因为四边形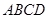 与
与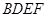 均为菱形,
均为菱形,
所以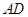 //
//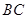 ,
,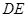 //
//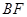 ,
,
所以 平面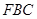 //平面
//平面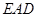 . ………………7分 又
. ………………7分 又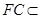 平面
平面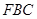 ,
,
所以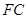 // 平面
// 平面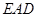 . ……………8分
. ……………8分
(Ⅲ)解:因为四边形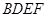 为菱形,且
为菱形,且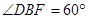 ,所以△
,所以△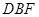 为等边三角形.
为等边三角形.
因为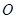 为
为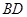 中点,所以
中点,所以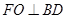 ,故
,故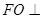 平面
平面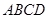 .
.
由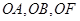 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系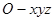 .………………9分
.………………9分
设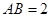 .因为四边形
.因为四边形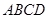 为菱形,
为菱形,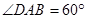 ,则
,则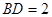 ,所以
,所以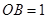 ,
,
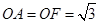 .
.
所以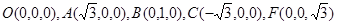 .
.
所以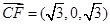 ,
,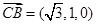 .
.
设平面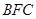 的法向量为
的法向量为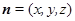 ,则有
,则有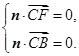
所以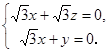 取
取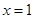 ,得
,得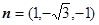 .………………12分
.………………12分
易知平面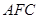 的法向量为
的法向量为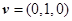 . ………………13分
. ………………13分
由二面角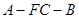 是锐角,得
是锐角,得 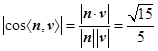 .
.
所以二面角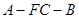 的余弦值为
的余弦值为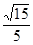 . ……………14分
. ……………14分
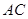 与
与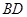 相交于点
相交于点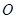 ,连结
,连结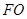 .
.因为 四边形
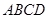 为菱形,所以
为菱形,所以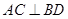 ,
,且
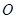 为
为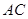 中点. ………………1分
中点. ………………1分又
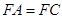 ,所以
,所以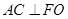 . ………3分
. ………3分因为
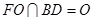 ,
, 所以
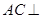 平面
平面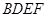 . ………………4分
. ………………4分 (Ⅱ)证明:因为四边形
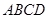 与
与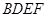 均为菱形,
均为菱形,所以
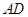 //
//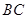 ,
,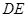 //
//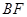 ,
,所以 平面
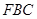 //平面
//平面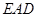 . ………………7分 又
. ………………7分 又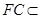 平面
平面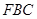 ,
,所以
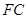 // 平面
// 平面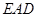 . ……………8分
. ……………8分 (Ⅲ)解:因为四边形
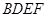 为菱形,且
为菱形,且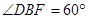 ,所以△
,所以△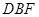 为等边三角形.
为等边三角形.因为
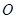 为
为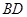 中点,所以
中点,所以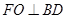 ,故
,故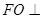 平面
平面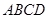 .
.由
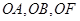 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系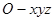 .………………9分
.………………9分 设
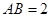 .因为四边形
.因为四边形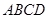 为菱形,
为菱形,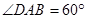 ,则
,则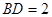 ,所以
,所以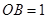 ,
,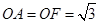 .
.所以
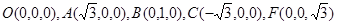 .
. 所以
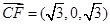 ,
,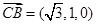 .
. 设平面
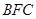 的法向量为
的法向量为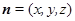 ,则有
,则有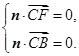
所以
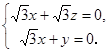 取
取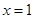 ,得
,得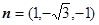 .………………12分
.………………12分 易知平面
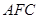 的法向量为
的法向量为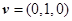 . ………………13分
. ………………13分 由二面角
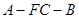 是锐角,得
是锐角,得 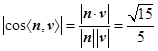 .
. 所以二面角
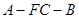 的余弦值为
的余弦值为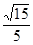 . ……………14分
. ……………14分略

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
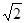 ,则球O的表面积为( )
,则球O的表面积为( )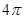 B、
B、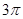 C、
C、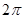 D、
D、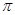
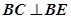 ;
;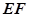 与平面
与平面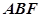 所成角的正弦值.
所成角的正弦值.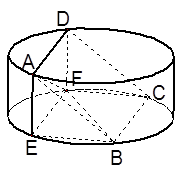
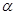 :A、B、C、D中有三个点到
:A、B、C、D中有三个点到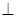 平面ABCD,M,N分别是AB,PC的中点。
平面ABCD,M,N分别是AB,PC的中点。
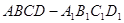 中,
中, 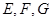 是
是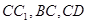 的中点
的中点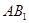 ∥平面
∥平面 ;
;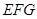 ∥平面
∥平面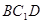
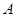 为端点的三条棱长都等于1,且它们彼此的夹角都是
为端点的三条棱长都等于1,且它们彼此的夹角都是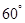 ,那么以这个顶点为端点的晶体的对角线的长为 。
,那么以这个顶点为端点的晶体的对角线的长为 。