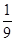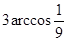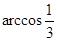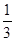题目内容
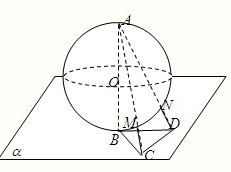
半径为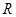 的球
的球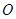 的直径
的直径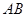 垂直于平面
垂直于平面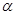 ,垂足为
,垂足为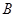 ,
,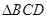 是平面
是平面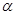 内边长为
内边长为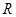 的正三角形,线段
的正三角形,线段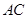 、
、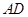 分别与球面交于点M,N,那么M、N两点间的球面距离是( )
分别与球面交于点M,N,那么M、N两点间的球面距离是( )
 的球
的球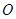 的直径
的直径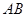 垂直于平面
垂直于平面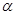 ,垂足为
,垂足为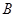 ,
,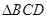 是平面
是平面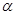 内边长为
内边长为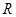 的正三角形,线段
的正三角形,线段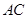 、
、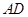 分别与球面交于点M,N,那么M、N两点间的球面距离是( )
分别与球面交于点M,N,那么M、N两点间的球面距离是( )A.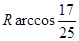 | B.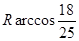 |
C.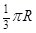 | D.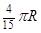 |

A
解:由已知,AB=2R,BC=R,
故tan∠BAC="1" /2,cos∠BAC=
连接OM,则△OAM为等腰三角形
AM=2AOcos∠BAC= R,
R,
同理AN= R,且MN∥CD
R,且MN∥CD
而AC= R,CD=R
R,CD=R
故MN:CD=AM:AC
MN= R,
R,
连接OM、ON,有OM=ON=R
于是cos∠MON="(OM2+ON2-MN2)" /2OM•ON ="17/" 25
所以M、N两点间的球面距离是Rarccos17 /25
故tan∠BAC="1" /2,cos∠BAC=

连接OM,则△OAM为等腰三角形
AM=2AOcos∠BAC=
 R,
R,同理AN=
 R,且MN∥CD
R,且MN∥CD而AC=
 R,CD=R
R,CD=R故MN:CD=AM:AC
MN=
 R,
R,连接OM、ON,有OM=ON=R
于是cos∠MON="(OM2+ON2-MN2)" /2OM•ON ="17/" 25
所以M、N两点间的球面距离是Rarccos17 /25

练习册系列答案
相关题目
 两点在平面
两点在平面 的同侧,
的同侧, 于
于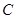 .
.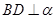 于
于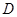 .
.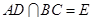 、
、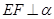 于
于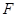 ,
,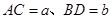 ,则
,则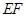 的长是( )
的长是( )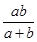
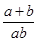
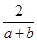

 是异面直线,那么和
是异面直线,那么和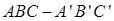 中,
中,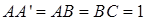 ,
,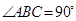 .棱
.棱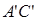 上有两个动点E,F,且EF = a (a为常数).
上有两个动点E,F,且EF = a (a为常数).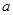
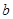
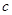
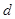
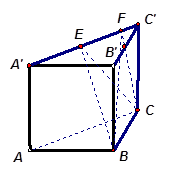
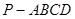 中,
中,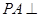 底面
底面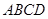 ,
,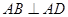 ,点E在线段AD上,且CE//AB。
,点E在线段AD上,且CE//AB。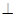 PAD;
PAD;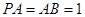 ,AD=3,CD=
,AD=3,CD=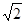 ,
,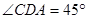 ,求四棱锥
,求四棱锥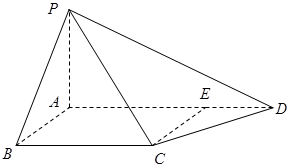
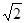 ,则球O的表面积为( )
,则球O的表面积为( )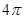 B、
B、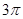 C、
C、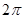 D、
D、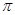
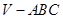 中,
中,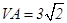 ,
,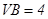 ,
,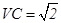 ,点
,点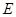 为侧棱
为侧棱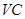 上的一点,
上的一点,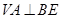 ,且顶点
,且顶点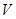 在底面
在底面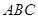 上的射影为底面的垂心.如果球
上的射影为底面的垂心.如果球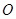 是三棱锥
是三棱锥 两点的球面距离是( )
两点的球面距离是( )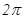
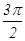
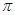
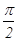
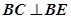 ;
;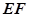 与平面
与平面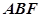 所成角的正弦值.
所成角的正弦值.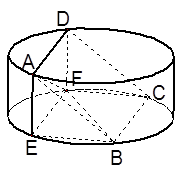
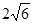 ,
,