题目内容
15.求下列函数的反函数,找出它们的定义域和值域.(1)y=2+lg(x+1);
(2)y=3+$\sqrt{x}$;
(3)y=$\frac{x-1}{x+1}$.
分析 (1)由对数式的真数大于0求出原函数的定义域,进一步求出原函数的值域,把原函数变形,化对数式为指数式,再把x,y互换求出原函数的反函数,得到反函数的定义域和值域;
(2)由根式内部的代数式大于等于0求出原函数的定义域,进一步求出原函数的值域,把原函数变形,求出x,再把x,y互换求出原函数的反函数,得到反函数的定义域和值域;
(3)由分式的分母不为0求出原函数的定义域,进一步求出原函数的值域,把原函数变形,求出x,再把x,y互换求出原函数的反函数,得到反函数的定义域和值域.
解答 解:(1)y=2+lg(x+1),
由x+1>0,可得x>-1,∴原函数的定义域为(-1,+∞),值域为R.
由y=2+lg(x+1),得lg(x+1)=y-2,化为指数式得,x+1=10y-2,
x,y互换得:y=10x-2-1,
此反函数的定义域为R,值域为(-1,+∞);
(2)y=3+$\sqrt{x}$,
由x≥0,可得原函数的定义域为[0,+∞),值域为[3,+∞).
由y=3+$\sqrt{x}$,得$\sqrt{x}=y-3$,x=(y-3)2,
x,y互换得:y=(x-3)2,
此反函数的定义域为[3,+∞),再由为[0,+∞);
(3)y=$\frac{x-1}{x+1}$,
由x+1≠0,得x≠-1,∴原函数的定义域为{x|x≠-1},
由y=$\frac{x-1}{x+1}$=$\frac{x+1-2}{x+1}=1-\frac{2}{x+1}$,∴原函数的值域为{y|y≠1}.
由y=$\frac{x-1}{x+1}$,得yx+y=x-1,即(1-y)x=1+y,∴x=$\frac{1+y}{1-y}$,
x与y互换得:$y=\frac{1+x}{1-x}$,
此反函数的定义域为{x|x≠1},值域为{y|y≠-1}.
点评 本题考查函数的反函数的求法,考查函数的定义域及其值域的求法,明确函数的反函数的定义域是原函数的值域是关键,是中档题.

| A. | -2 | B. | 2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
(1)求f(x)的解析式;
(2)设函数h(x)=2f(x-$\frac{π}{12}$),x∈[$-\frac{π}{4}$,$\frac{π}{4}$],求h(x)的最大值和最小值.
| x | $-\frac{π}{4}$ | 0 | $\frac{π}{6}$ | $\frac{π}{4}$ | $\frac{π}{2}$ | $\frac{3π}{4}$ |
| f(x) | 0 | 1 | $\frac{1}{2}$ | 0 | -1 | 0 |
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | 2 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图,四边形ABCD是正方形,SA=SB=SC=SD,P是棱SC上的点,M,N分别是棱SB,SD上的点,SP:PC=1:2,SN:ND=2:1,SM:MB=2:1
如图,四边形ABCD是正方形,SA=SB=SC=SD,P是棱SC上的点,M,N分别是棱SB,SD上的点,SP:PC=1:2,SN:ND=2:1,SM:MB=2:1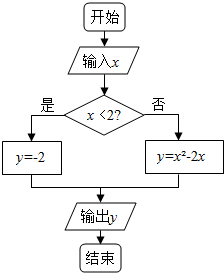 据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题
据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题