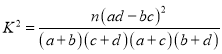题目内容
【题目】已知函数f(x)=ax﹣sinx(a∈R).
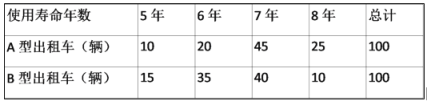
(1)当![]() 时,f(x)
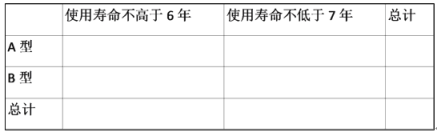
时,f(x)![]() 0恒成立,求正实数a的取值范围;
0恒成立,求正实数a的取值范围;
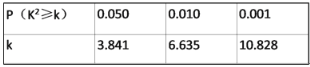
(2)当a≥1时,探索函数F(x)![]() f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由已知分离参数后构造函数,转化为求解函数的最值或范围,结合导数可求;
(2)由已知结合导数分析函数的性质,然后结合函数的零点判定定理可求.
解:(1)因为![]() ,
,
所以![]() ,
,
令![]() ,
,![]() ,
,
再令m(x)![]() xcosx﹣sinx,m'(x)
xcosx﹣sinx,m'(x)![]() cosx﹣xsinx﹣cosx
cosx﹣xsinx﹣cosx![]() ﹣xsinx
﹣xsinx![]() 0,
0,
所以m(x)在(0,![]() )上单调递减,
)上单调递减,
所以m(x)![]() m(0)=0.
m(0)=0.
所以g'(x)![]() 0,则g(x)在(0,
0,则g(x)在(0,![]() )上单调递减,
)上单调递减,
所以g(x)![]() g(
g(![]() )
)![]() ,
,
所以a![]() ,
,
又a![]() 0,
0,
即正实数a的取值范围是(0,![]() ].
].
(2)F(x)![]() f(x)﹣cosx+a﹣1
f(x)﹣cosx+a﹣1![]() ax﹣sinx﹣cosx+a﹣1,
ax﹣sinx﹣cosx+a﹣1,
则![]() ,
,
因为x∈(0,π),
故![]() ,
,
又a≥1,
故F′(x)![]() 0对x∈(0,π)恒成立,
0对x∈(0,π)恒成立,
即F(x)在区间(0,π)单调递增;
又F(0)=a﹣2,F(π)=a(1+π)![]() 0,
0,
故当1≤a![]() 2时,F(0)=a﹣2
2时,F(0)=a﹣2![]() 0,此时F(x)在区间(0,π)内恰好有1个零点;
0,此时F(x)在区间(0,π)内恰好有1个零点;
当a≥2时,F(0)=a﹣2≥0,此时F(x)在区间(0,π)内没有零点.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目