题目内容
15.将函数y=cos(2x+$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位后,得到f(x)的图象,则( )| A. | f(x)=-sin2x | B. | f(x)的图象关于x=-$\frac{π}{3}$对称 | ||
| C. | f($\frac{7π}{3}$)=$\frac{1}{2}$ | D. | f(x)的图象关于($\frac{π}{12}$,0)对称 |
分析 利用诱导公式、y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质,得出结论.
解答 解:将函数y=cos(2x+$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位后,得到f(x)=cos[2(x+$\frac{π}{6}$)+$\frac{π}{3}$]
=cos(2x+$\frac{2π}{3}$)=-sin(2x+$\frac{π}{6}$)的图象,故排除A;
当x=-$\frac{π}{3}$时,f(x)=1,为最大值,故f(x)的图象关于x=-$\frac{π}{3}$对称,故B正确;
f($\frac{7π}{3}$)=-sin$\frac{29π}{6}$=-sin$\frac{5π}{6}$=-$\frac{1}{2}$,故排除C;
当x=$\frac{π}{12}$时,f(x)=-sin$\frac{π}{3}$=-$\frac{\sqrt{3}}{2}$≠0,故f(x)的图象不关于($\frac{π}{12}$,0)对称,故D错误,
故选:B.
点评 本题主要考查诱导公式的应用,利用了y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
3.将函数y=sin(x+$\frac{π}{6}$)的图象上所有的点向左平移$\frac{π}{4}$个的单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得图象的解析式为( )
| A. | y=sin(2x+$\frac{5π}{12}$) | B. | y=sin($\frac{x}{2}$+$\frac{5π}{12}$) | C. | y=sin ($\frac{x}{2}$-$\frac{π}{12}$) | D. | y=sin($\frac{x}{2}$+$\frac{5π}{24}$) |
4.若复数z满足z(4-i)=5+3i(i为虚数单位),则$\overline z$为( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | -1-i |
 在如图所示的几何体中,平面ADNM⊥平面ABCD,四边形ABCD是菱形,ADNM是矩形,$∠DAB=\frac{π}{3}$,AB=2,AM=1,E是AB的中点.
在如图所示的几何体中,平面ADNM⊥平面ABCD,四边形ABCD是菱形,ADNM是矩形,$∠DAB=\frac{π}{3}$,AB=2,AM=1,E是AB的中点.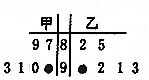 在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图:
在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图: