题目内容
1.在△ABC,角A、B、C所对的边分别为a、b、c,已知cosB+(cosA-2sinA)cosC=0.(Ⅰ)求cosC的值;
(Ⅱ)若$a=\sqrt{5}$,AC边上的中线$BM=\frac{{\sqrt{17}}}{2}$,求△ABC的面积.
分析 (Ⅰ)由题意和和差角的三角函数公式可得tanC=2,再由同角三角函数基本关系可得;
(Ⅱ)在△ABC中,由余弦定理可得b2-4b+3=0,解方程分别由三角形的面积公式可得.
解答 解:(Ⅰ)在△ABC,∵cosB=-cos(A+C)=-cosAcosC+sinAsinC,
又∵cosB+(cosA-2sinA)cosC=0,
∴sinAsinC-2sinAcosC=0,
∵sinA≠0,∴sinC-2cosC=0,
∴tanC=2,由同角三角函数基本关系可得$cosC=\frac{{\sqrt{5}}}{5}$;
(Ⅱ)在△ABC中,由余弦定理得BM2=BC2+CM2-2BC•CMcosC,
代入数据可得b2-4b+3=0,解得b=1或b=3,
当b=1时,△ABC的面积$S=\frac{1}{2}absinC=1$;
当b=3时,△ABC的面积$S=\frac{1}{2}absinC=3$.
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式和分类讨论思想,属中档题.

练习册系列答案
相关题目
13.若集合M={x|$\frac{1}{x}$<2},集合N={x|-1<x<2},则M∩N等于( )
| A. | {x|$\frac{1}{2}$<x<2} | B. | {x|-1<x<0或$\frac{1}{2}$<x<2} | C. | {x|-1<x<$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$或1<x<2} |
10.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验,收集数据如表所示,根据右表可得回归方程$\hat y=\hat bx+\hat a$中的$\hat b$为9.4,据此可估计加工零件数为6时加工时间大约为( )
| 零件数x(个) | 2 | 3 | 4 | 5 |
| 加工时间y(min) | 26 | 39 | 49 | 54 |
| A. | 63.6 min | B. | 65.5 min | C. | 67.7 min | D. | 72.0 min |
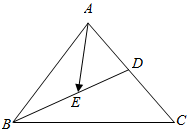 如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.
如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.