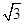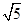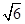题目内容
(本小题满分12分)
已知曲线 上的点到点
上的点到点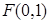 的距离比它到直线
的距离比它到直线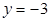 的距离小2.
的距离小2.
(1)求曲线 的方程;
的方程;
(2)曲线 在点
在点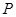 处的切线
处的切线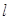 与
与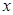 轴交于点
轴交于点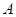 .直线
.直线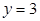 分别与直线
分别与直线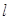 及
及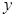 轴交于点
轴交于点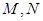 ,以
,以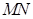 为直径作圆
为直径作圆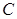 ,过点
,过点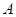 作圆
作圆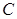 的切线,切点为
的切线,切点为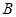 ,试探究:当点
,试探究:当点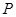 在曲线
在曲线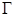 上运动(点
上运动(点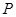 与原点不重合)时,线段
与原点不重合)时,线段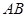 的长度是否发生变化?证明你的结论.
的长度是否发生变化?证明你的结论.
已知曲线
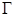 上的点到点
上的点到点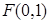 的距离比它到直线
的距离比它到直线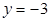 的距离小2.
的距离小2.(1)求曲线
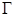 的方程;
的方程;(2)曲线
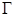 在点
在点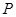 处的切线
处的切线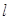 与
与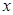 轴交于点
轴交于点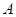 .直线
.直线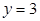 分别与直线
分别与直线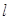 及
及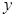 轴交于点
轴交于点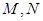 ,以
,以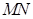 为直径作圆
为直径作圆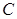 ,过点
,过点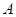 作圆
作圆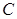 的切线,切点为
的切线,切点为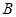 ,试探究:当点
,试探究:当点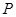 在曲线
在曲线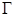 上运动(点
上运动(点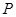 与原点不重合)时,线段
与原点不重合)时,线段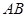 的长度是否发生变化?证明你的结论.
的长度是否发生变化?证明你的结论.(1)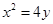 .(2)当点P在曲线
.(2)当点P在曲线 上运动时,线段AB的长度不变,证明见解析.
上运动时,线段AB的长度不变,证明见解析.
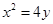 .(2)当点P在曲线
.(2)当点P在曲线 上运动时,线段AB的长度不变,证明见解析.
上运动时,线段AB的长度不变,证明见解析.试题分析:(1)思路一:设
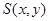 为曲线
为曲线 上任意一点,
上任意一点,依题意可知曲线
 是以点
是以点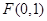 为焦点,直线
为焦点,直线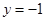 为准线的抛物线,
为准线的抛物线,得到曲线
 的方程为
的方程为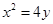 .
.思路二:设
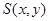 为曲线
为曲线 上任意一点,
上任意一点,由
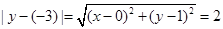 ,化简即得.
,化简即得.(2)当点P在曲线
 上运动时,线段AB的长度不变,证明如下:
上运动时,线段AB的长度不变,证明如下:由(1)知抛物线
 的方程为
的方程为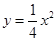 ,
,设
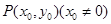 ,得
,得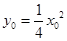 ,
,应用导数的几何意义,确定切线的斜率,进一步得切线
 的方程为
的方程为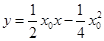 .
.由
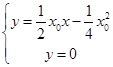 ,得
,得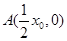 .
.由
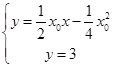 ,得
,得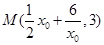 .
.根据
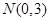 ,得圆心
,得圆心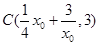 ,半径
,半径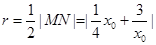 ,
,由弦长,半径及圆心到直线的距离之关系,确定
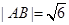 .
.试题解析:解法一:(1)设
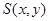 为曲线
为曲线 上任意一点,
上任意一点,依题意,点S到
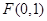 的距离与它到直线
的距离与它到直线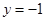 的距离相等,
的距离相等,所以曲线
 是以点
是以点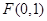 为焦点,直线
为焦点,直线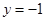 为准线的抛物线,
为准线的抛物线,所以曲线
 的方程为
的方程为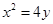 .
.(2)当点P在曲线
 上运动时,线段AB的长度不变,证明如下:
上运动时,线段AB的长度不变,证明如下:由(1)知抛物线
 的方程为
的方程为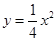 ,
,设
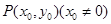 ,则
,则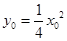 ,
,由
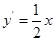 ,得切线
,得切线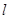 的斜率
的斜率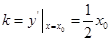 ,
,所以切线
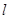 的方程为
的方程为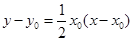 ,即
,即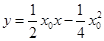 .
.由
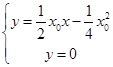 ,得
,得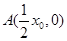 .
.由
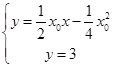 ,得
,得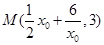 .
.又
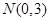 ,所以圆心
,所以圆心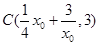 ,
,半径
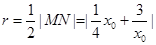 ,
,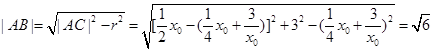 .
.所以点P在曲线
 上运动时,线段AB的长度不变.
上运动时,线段AB的长度不变.
解法二:
(1)设
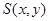 为曲线
为曲线 上任意一点,
上任意一点,则
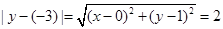 ,
,依题意,点
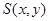 只能在直线
只能在直线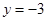 的上方,所以
的上方,所以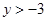 ,
,所以
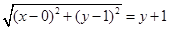 ,
,化简得,曲线
 的方程为
的方程为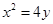 .
.(2)同解法一.

练习册系列答案
相关题目
 的右焦点为
的右焦点为 ,
,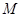 为上顶点,
为上顶点,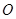 为坐标原点,若△
为坐标原点,若△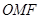 的面积为
的面积为 ,且椭圆的离心率为
,且椭圆的离心率为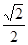 .
.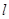 交椭圆于
交椭圆于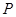 ,
,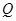 两点, 且使点
两点, 且使点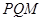 的垂心?若存在,求出直线
的垂心?若存在,求出直线 中,椭圆
中,椭圆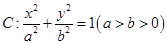 的离心率为
的离心率为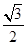 ,直线
,直线 被椭圆
被椭圆 截得的线段长为
截得的线段长为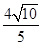 .
. 两点(
两点( 在椭圆
在椭圆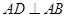 ,直线
,直线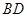 与
与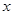 轴、
轴、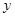 轴分别交于
轴分别交于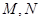 两点.
两点.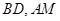 的斜率分别为
的斜率分别为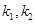 ,证明存在常数
,证明存在常数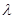 使得
使得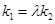 ,并求出
,并求出 面积的最大值.
面积的最大值.
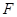 是抛物线
是抛物线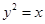 的焦点,点
的焦点,点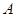 ,
,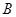 在该抛物线上且位于
在该抛物线上且位于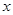 轴的两侧,
轴的两侧,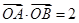 (其中
(其中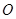 为坐标原点),则
为坐标原点),则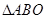 与
与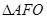 面积之和的最小值是( )
面积之和的最小值是( )
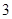
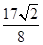
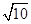
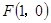 的距离和到直线
的距离和到直线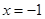 的距离相等.若机器人接触不到过点
的距离相等.若机器人接触不到过点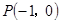 且斜率为
且斜率为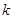 的直线,则
的直线,则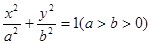 的左右顶点分别为
的左右顶点分别为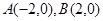 ,离心率
,离心率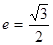 .
.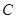 为曲线
为曲线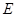 :
: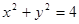 上任一点(
上任一点(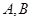 ),直线
),直线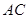 与直线
与直线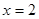 交于点
交于点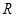 ,
,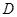 为线段
为线段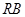 的中点,试判断直线
的中点,试判断直线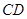 与曲线
与曲线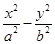 =1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率等于( )
=1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率等于( )