题目内容
(本小题满分14分)
在平面直角坐标系 中,椭圆
中,椭圆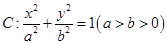 的离心率为
的离心率为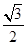 ,直线
,直线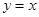 被椭圆
被椭圆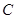 截得的线段长为
截得的线段长为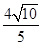 .
.
(Ⅰ)求椭圆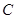 的方程;
的方程;
(Ⅱ)过原点的直线与椭圆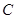 交于
交于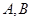 两点(
两点(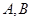 不是椭圆
不是椭圆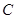 的顶点).点
的顶点).点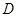 在椭圆
在椭圆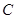 上,且
上,且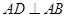 ,直线
,直线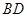 与
与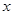 轴、
轴、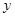 轴分别交于
轴分别交于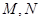 两点.
两点.
(i)设直线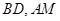 的斜率分别为
的斜率分别为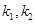 ,证明存在常数
,证明存在常数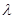 使得
使得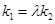 ,并求出
,并求出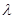 的值;
的值;
(ii)求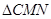 面积的最大值.
面积的最大值.
在平面直角坐标系
 中,椭圆
中,椭圆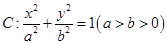 的离心率为
的离心率为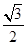 ,直线
,直线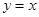 被椭圆
被椭圆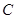 截得的线段长为
截得的线段长为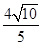 .
.(Ⅰ)求椭圆
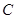 的方程;
的方程;(Ⅱ)过原点的直线与椭圆
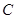 交于
交于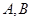 两点(
两点(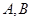 不是椭圆
不是椭圆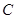 的顶点).点
的顶点).点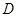 在椭圆
在椭圆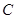 上,且
上,且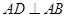 ,直线
,直线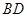 与
与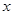 轴、
轴、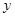 轴分别交于
轴分别交于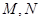 两点.
两点.(i)设直线
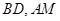 的斜率分别为
的斜率分别为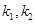 ,证明存在常数
,证明存在常数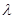 使得
使得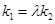 ,并求出
,并求出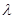 的值;
的值;(ii)求
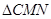 面积的最大值.
面积的最大值.(1) .(2)(ⅰ)存在常数
.(2)(ⅰ)存在常数 使得结论成立.(ⅱ)
使得结论成立.(ⅱ) .
.
 .(2)(ⅰ)存在常数
.(2)(ⅰ)存在常数 使得结论成立.(ⅱ)
使得结论成立.(ⅱ) .
.试题分析:(1)首先由题意得到
 ,即
,即 .
.将
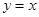 代入
代入 可得
可得 ,
,由
 ,可得
,可得 .
. 得解.
得解.(2)(ⅰ)注意从确定
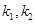 的表达式入手,探求使
的表达式入手,探求使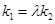 成立的
成立的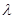 .
.设
 ,则
,则 ,
,得到
 ,
,根据直线BD的方程为
 ,
,令
 ,得
,得 ,即
,即 .得到
.得到 .
.由
 ,作出结论.
,作出结论.(ⅱ)直线BD的方程
 ,
,从确定
 的面积表达式
的面积表达式 入手,应用基本不等式得解.
入手,应用基本不等式得解.试题解析:(1)由题意知
 ,可得
,可得 .
.椭圆C的方程可化简为
 .
.将
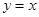 代入可得
代入可得 ,
,因此
 ,可得
,可得 .
.因此
 ,
,所以椭圆C的方程为
 .
.(2)(ⅰ)设
 ,则
,则 ,
,因为直线AB的斜率
 ,
,又
 ,所以直线AD的斜率
,所以直线AD的斜率 ,
,设直线AD的方程为
 ,
,由题意知
 ,
,由
 ,可得
,可得 .
.所以
 ,
,因此
 ,
,由题意知,

所以
 ,
,所以直线BD的方程为
 ,
,令
 ,得
,得 ,即
,即 .
.可得
 .
.所以
 ,即
,即 .
.因此存在常数
 使得结论成立.
使得结论成立.(ⅱ)直线BD的方程
 ,
,令
 ,得
,得 ,即
,即 ,
,由(ⅰ)知
 ,
,可得
 的面积
的面积 ,
,因为
 ,当且仅当
,当且仅当 时等号成立,
时等号成立,此时S取得最大值
 ,
,所以
 的面积的最大值为
的面积的最大值为 .
.
练习册系列答案
相关题目

 上的点到点
上的点到点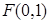 的距离比它到直线
的距离比它到直线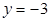 的距离小2.
的距离小2. 处的切线
处的切线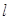 与
与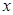 轴交于点
轴交于点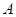 .直线
.直线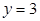 分别与直线
分别与直线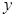 轴交于点
轴交于点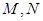 ,以
,以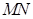 为直径作圆
为直径作圆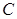 ,过点
,过点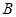 ,试探究:当点
,试探究:当点 的长度是否发生变化?证明你的结论.
的长度是否发生变化?证明你的结论.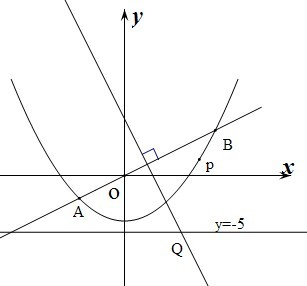
 相切于点P(2,1),且与
相切于点P(2,1),且与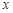 轴交于点A,定点B的坐标为(2,0) .
轴交于点A,定点B的坐标为(2,0) .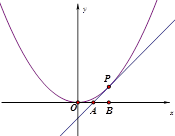
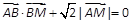 ,求点M的轨迹C;
,求点M的轨迹C;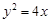 的焦点为
的焦点为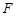 ,点
,点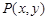 为该抛物线上的动点,又点
为该抛物线上的动点,又点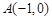 ,
,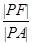 的取值范围是 .
的取值范围是 . 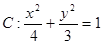 ,直线
,直线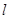 的方程为
的方程为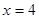 ,过右焦点
,过右焦点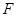 的直线
的直线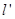 与椭圆交于异于左顶点
与椭圆交于异于左顶点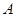 的
的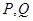 两点,直线
两点,直线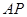 ,
,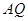 交直线
交直线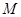 ,
,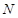 .
.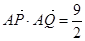 时,求此时直线
时,求此时直线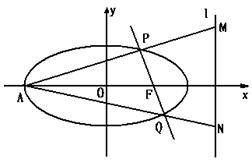
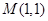 作斜率为
作斜率为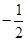 的直线与椭圆
的直线与椭圆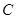 :
: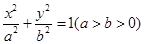 相交于
相交于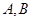 ,若
,若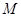 是线段
是线段 的中点,则椭圆
的中点,则椭圆