Question

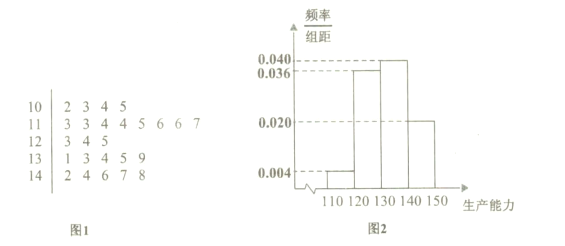
【题目】某工厂有工人1000名，为了提高工人的生产技能，特组织工人参加培训.其中250名工人参加过短期培训（称为类工人），另外750名工人参加过长期培训（称为类工人）.现从该工厂的工人中共抽查了100名工人作为样本，调查他们的生产能力（生产能力是指工人一天加工的零件数），得到类工人生产能力的茎叶图（图1），类工人生产能力的频率分布直方图（图2）.

（1）在样本中求类工人生产能力的中位数，并估计类工人生产能力的平均数（同一组中的数据用该组区间的中点值作代表）；

（2）若规定生产能力在内为能力优秀，现以样本中频率作为概率，从1000名工人中按分层抽样共抽取名工人进行调查，请估计这名工人中的各类人数，完成下面的列联表.

若研究得到在犯错误的概率不超过的前提下，认为生产能力与培训时间长短有关，则的最小值为多少？

参考数据：

参考公式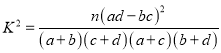： ，其中.

Answer 1

【答案】（1）132.6；（2）360

【解析】试题分析：（1）由茎叶图知A类工人生产能力的中位数，由频率分布直方图，估计出B类工人生产能力的平均数；

（2）列出能力与培训的列联表，计算卡方，结合表格作出判断.

试题解析：

（1）由茎叶图知类工人生产能力的中位数为123，由频率分布直方图，估计类工人生产能力的平均数为 ；

（2）由（1）及所给数据得能力与培训的列联表如下：

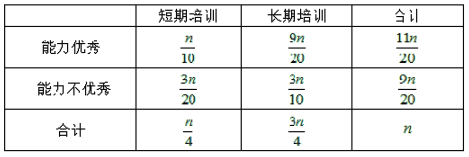
由上表得

，

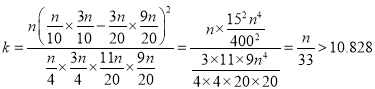解得，又人数必须取整，

∴的最小值为360.