题目内容

16．已知集合A={-1，0，1，2，3，4}，B={x|x2＜16，x∈N}，则A∩B等于（　　）
A．{-1，0，1，2，3}B．{0，1，2，3，4}C．{1，2，3}D．{0，1，2，3}

分析 解不等式得出B，根据交集的运算写出A∩B．

解答 解：集合A={-1，0，1，2，3，4}，
B={x|x2＜16，x∈N}={x|-4＜x＜4，x∈N}，
则A∩B={0，1，2，3}．
故选：D．

点评 本题考查了解不等式与集合的基本运算问题，是基础题．

练习册系列答案
相关题目
6．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0），右焦点$F（\sqrt{2}，0）$，点$D（\sqrt{2}，1）$在椭圆上；
（1）求椭圆C的标准方程；
（2）是否存在过原点的直线l与椭圆C交于A、B两点，且∠AFB=90°？若存在，请求出所有符合要求的直线；若不存在，请说明理由．
7．直线ax+by=1（b≥-1）和以A（1，0），B（2，1）为端点的线段相交，则$\frac{b}{a}$取不到的值为（　　）
A．-1B．-2C．-$\frac{1}{2}$D．1
4．某三棱锥的三视图如图所示，则该三棱锥的体积为（　　）
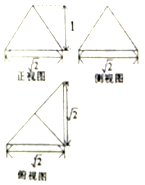
A．$\frac{2}{3}$B．1C．$\frac{1}{3}$D．2
11．已知函数$f（x）=\frac{2}{3}{x^3}+a{x^2}-（a-b）x+c$的两个极值点分别为x1，x2，且x1∈（-∞，-1），x2∈（-1，0），点P（a，b）表示的平面区域为D，若函数y=logm（x+2）（m＞0，m≠1）的图象经过区域D，则实数m的取值范围是（　　）
A．（3，+∞）B．[3，+∞）C．（1，3）D．（1，3]
1．求曲线y=$\frac{1}{\sqrt{{x}^{2}-3x}}$在点（4，$\frac{1}{2}$）处的切线方程．
8．若$f（x）=\left\{{\begin{array}{l}{f（x-5），x＞0}\\{{2^x}+\int_0^{\frac{π}{6}}{cos3tdt，x≤0}}\end{array}}\right.$，则f（2017）=（　　）
A．$\frac{1}{24}$B．$\frac{11}{24}$C．$\frac{5}{6}$D．$\frac{1}{2}$
5．在△ABC中，角A，B，C所对的边分别是a，b，c，且sin2A-sin（2B+C）=sinC．
（1）证明：a=b；
（2）若A为函数f（x）=sin（$\frac{π}{4}$-x）sin（$\frac{π}{4}$+x）+$\frac{1}{4}$的一个零点，且c=2，求△ABC的面积．
6．已知函数f（x）=|x+a|+|x-2|的定义域为实数集R．
（Ⅰ）当a=5时，解关于x的不等式f（x）＞9；
（Ⅱ）设关于x的不等式f（x）≤|x-4|的解集为A，B={x∈R|2x-1|≤3}，如果A∪B=A，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网