题目内容
3.若数列{an}满足:a1=2,an+1=$\frac{{a}_{n}-1}{{a}_{n}}$,则a7等于( )| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2018 |
分析 利用数列的递推关系式,逐步求解即可.
解答 解:数列{an}满足:a1=2,an+1=$\frac{{a}_{n}-1}{{a}_{n}}$,则a2=$\frac{2-1}{2}$=$\frac{1}{2}$,
a3=$\frac{\frac{1}{2}-1}{\frac{1}{2}}$=-1
a4=$\frac{-1-1}{-1}$=2
a5=$\frac{2-1}{2}$=$\frac{1}{2}$,
a6=$\frac{\frac{1}{2}-1}{\frac{1}{2}}$=-1.
a7=$\frac{-1-1}{-1}$=2.
故选:A.
点评 本题考查数列的递推关系式的应用,考查计算能力.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
13.将函数f(x)的图象向左平移$\frac{π}{6}$个单位后得到函数g(x)的图象如图所示,则函数f(x)的解析式是( )
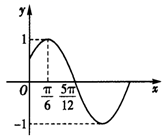

| A. | $f(x)=sin({2x-\frac{π}{6}})$(x∈R) | B. | $f(x)=sin({2x+\frac{π}{6}})$(x∈R) | C. | $f(x)=sin({2x-\frac{π}{3}})$(x∈R) | D. | $f(x)=sin({2x+\frac{π}{3}})$(x∈R) |
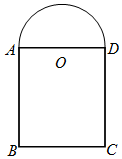 设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).
设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).