题目内容
设两非零向量
、
不共线，且k
+
与
+k
共线，则k的值为 ．
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
考点：平行向量与共线向量
专题：平面向量及应用
分析：利用平行向量的性质求解．
解答：
解：∵两非零向量
、
不共线，且k
+
与
+k
共线，
∴k
+
=t（
+k
）
则（k-t）
+（1-tk）
=0．
∵非零向量
、
不共线，
∴k-t=0，1-kt=0，解得k=±1．
故答案为：±1．
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
∴k
| e1 |
| e2 |
| e1 |
| e2 |
则（k-t）
| e1 |
| e2 |
∵非零向量
| e1 |
| e2 |
∴k-t=0，1-kt=0，解得k=±1．
故答案为：±1．
点评：本题考查满足条件的实数值的求法，解题时要注意平行向量的性质的灵活运用，是基础题．
练习册系列答案
相关题目
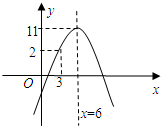某汽车运输公司，购买了一批豪华大客车投入客运，据市场分析，每辆客车营运的总利润y（万元）与营运年数x（x∈N*）的二次函数关系如图，为了使每辆客车营运的年平均利润最大，则每辆客车应营运