题目内容
15.在△ABC中,若角A、B、C的对边分别为a、b、c,且(a2+b2-c2)sinA=ab(2sinB+sinC).(1)求A;
(2)若a=1,求b+c的取值范围.
分析 (1)(a2+b2-c2)sinA=ab(2sinB+sinC),利用正弦定理可得:(a2+b2-c2)a=ab(2b+c),化简再利用余弦定理即可得出.
(2)由余弦定理可得:${a}^{2}={b}^{2}+{c}^{2}-2bccos\frac{2π}{3}$,再利用基本不等式的性质即可得出.
解答 解:(1)∵(a2+b2-c2)sinA=ab(2sinB+sinC),利用正弦定理可得:(a2+b2-c2)a=ab(2b+c),化为b2+c2-a2=-bc.
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$-\frac{1}{2}$,
A∈(0,π),∴$A=\frac{2π}{3}$.
(2)由余弦定理可得:${a}^{2}={b}^{2}+{c}^{2}-2bccos\frac{2π}{3}$,
∴1=(b+c)2-bc,即(b+c)2=1+bc≤1+$(\frac{b+c}{2})^{2}$,b+c>a=1.
解得:1<b+c≤$\frac{2\sqrt{3}}{3}$.
∴b+c的取值范围是$(1,\frac{2\sqrt{3}}{3}]$.
点评 本题考查了正弦定理余弦定理、三角函数求值、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
3.设全集U={1,2,3,4,5},A={1,5},B={2,4},则B∩(∁UA)=( )
| A. | {2,3,4} | B. | {2} | C. | {2,4} | D. | {1,3,4,5} |
4.方程lnx=$\frac{x+1}{x-1}$实数根的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
15.矩形ABCD中,AB=4,BC=2,M为AB的中点,在长方形ABCD内随机取一点P,取到的点P到M的距离大于2的概率为( )
| A. | $\frac{π}{2}$ | B. | $1-\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | $1-\frac{π}{4}$ |
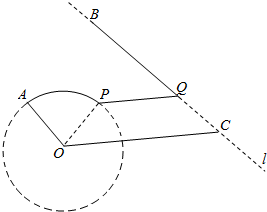 如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上.
如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上. 函数y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分如图所示:
函数y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分如图所示: