题目内容
已知数列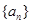 的前
的前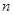 项和为
项和为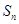 ,点
,点 在直线
在直线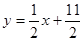 上.数列
上.数列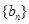 满足
满足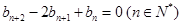 ,且
,且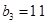 ,前9项和为153.
,前9项和为153.
(1)求数列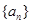 、
、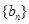 {的通项公式;
{的通项公式;
(2)设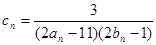 ,数列
,数列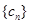 的前
的前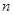 和为
和为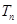 ,求使不等式
,求使不等式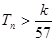 对一切
对一切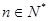 都成立的最大正整数
都成立的最大正整数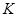 的值;
的值;
(3)设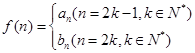 ,问是否存在
,问是否存在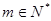 ,使得
,使得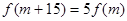 成立?若存在,求出
成立?若存在,求出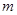 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)
 =
=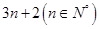 (2)
(2)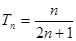
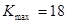
(3)存在唯一正整数m =11,使得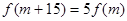 成立.
成立.
解析试题分析:(1)由题意,得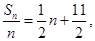 即
即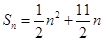
故当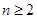 时,
时,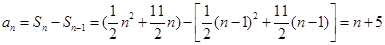
当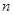 =1时,
=1时,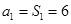 ,而当
,而当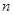 =1时,
=1时,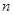 +5=6,
+5=6,
所以,
又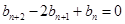 ,即
,即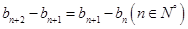
所以( )为等差数列,于是
)为等差数列,于是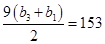
而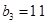 ,
,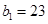 ,
,
因此, =
=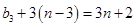 ,即
,即 =
=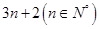
(2)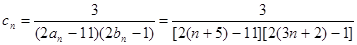
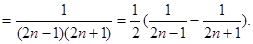
所以,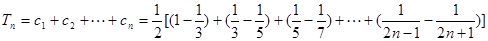
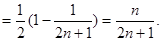
由于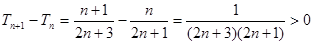 ,
,
因此Tn单调递增,故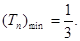
令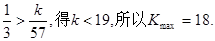
(Ⅲ)
①当m为奇数时,m + 15为偶数.
此时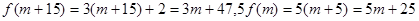 ,
,
所以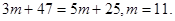
②当m为偶数时,m + 15为奇数.
此时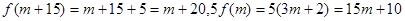 ,
,
所以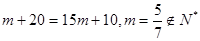 (舍去).
(舍去).
综上,存在唯一正整数m =11,使得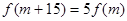 成立.
成立.
考点:数列递推式;等差关系的确定;数列的求和.
点评:本题考查数列的通项与求和,考查裂项法的运用,确定数列的通项是关键.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错,是高考的重点.

练习册系列答案
相关题目
 满足
满足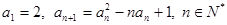 .
.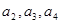 ,并由此猜想
,并由此猜想 的一个通项公式,证明你的结论;
的一个通项公式,证明你的结论;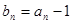 ,不等式
,不等式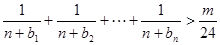 对一切
对一切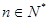 都成立,求正整数m的最大值。
都成立,求正整数m的最大值。 ,其前
,其前 项和
项和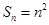 ,数列
,数列 满足
满足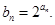
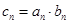 ,求数列
,求数列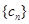 的前
的前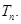
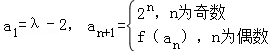 .
.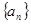 的前
的前 项和为
项和为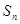
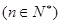 ,设
,设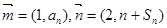 ,且
,且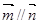 .
.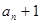 }是等比数列;
}是等比数列;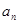 与
与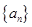 的相邻两项
的相邻两项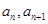 是关于
是关于 的方程
的方程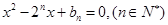 的两根,且
的两根,且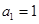 .
.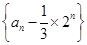 是等比数列;
是等比数列; 项和
项和 ;
;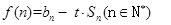 若
若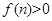 对任意的
对任意的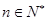 都成立,求
都成立,求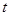 的取值范围。
的取值范围。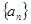 中,
中, 且点
且点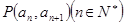 在直线
在直线 上。
上。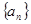 的通项公式;
的通项公式; (2)
(2)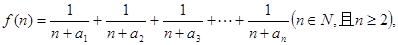 求函数
求函数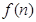 的最小值;
的最小值;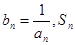 表示数列
表示数列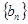 的前
的前 项和。试问:是否存在关于
项和。试问:是否存在关于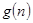 ,使得
,使得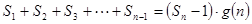 对于一切不小于2的自然数
对于一切不小于2的自然数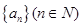 满足
满足 且对一切
且对一切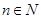 ,有
,有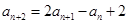
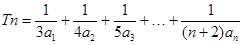 ,求
,求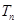 的取值范围.
的取值范围.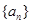 是公差为正的等差数列,其前
是公差为正的等差数列,其前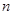 项和为
项和为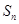 ,点
,点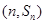 在抛物线
在抛物线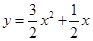 上;各项都为正数的等比数列
上;各项都为正数的等比数列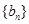 满足
满足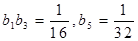 .
.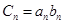 ,求数列
,求数列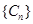 的前n项和
的前n项和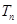 .
.