题目内容
设数列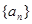 满足
满足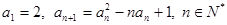 .
.
(Ⅰ)求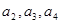 ,并由此猜想
,并由此猜想 的一个通项公式,证明你的结论;
的一个通项公式,证明你的结论;
(II)若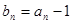 ,不等式
,不等式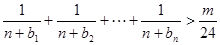 对一切
对一切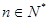 都成立,求正整数m的最大值。
都成立,求正整数m的最大值。
(I)

 ,猜想
,猜想 ,用数学归纳法证明。
,用数学归纳法证明。
(II)
解析试题分析:(I)由 得
得 ,
,
由 得
得 ,由
,由 得
得
由此猜想 ,
,
下面用数学归纳法证明
(1)当 时,
时, ,猜想成立。
,猜想成立。
(2)假设当 时,猜想成立,即
时,猜想成立,即
那么当 时,
时,
所以,当 时,猜想也成立。
时,猜想也成立。
由(1)(2)知,对于任意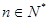 都有
都有 成立。
成立。
(II) 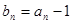 =n,则
=n,则
设

=
= 


考点:数列的递推公式,数学归纳法。
点评:中档题,本题解的思路较为清晰。涉及数列不等式的证明问题,提供了数学归纳法这一证明方法,利用递推公式计算要准确,应用数学归纳法证明,要注意规范性---“两步一结”,且必须应用归纳假设。

练习册系列答案
相关题目
 ,数列
,数列 前
前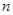 项和
项和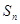 ,
,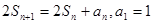 ,数列
,数列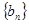 ,满足
,满足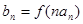 .(Ⅰ)求数列
.(Ⅰ)求数列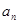 ;
;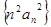 的前
的前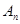 ,数列
,数列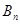 ,证明:
,证明: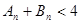 。
。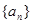 是各项都为正数的等比数列,
是各项都为正数的等比数列, 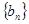 是等差数列,且
是等差数列,且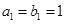 ,
,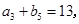
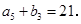
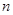 项和为
项和为 ,求数列
,求数列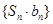 的前
的前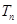 .
.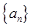 是首项
是首项 的等比数列,且
的等比数列,且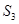 ,
,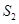 ,
, 成等差数列.
成等差数列.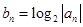 ,设
,设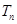 为数列
为数列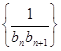 的前
的前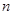 项和,若
项和,若 对一切
对一切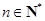 恒
恒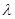 的最小值.
的最小值.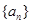 中,
中,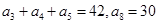 .
.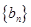 满足
满足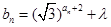 (
( ),则是否存在这样的实数
),则是否存在这样的实数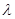 使得
使得 满足
满足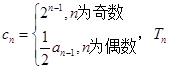 为数列
为数列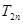 .
.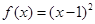 ,数列
,数列 是公差为d的等差数列,
是公差为d的等差数列,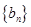 是公比为q(
是公比为q(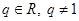 )的等比数列.若
)的等比数列.若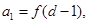
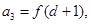

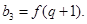
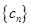 对任意自然数n均有
对任意自然数n均有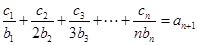 ,求
,求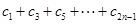 的值;
的值;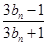 与
与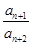 的大小.
的大小.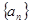 前
前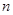 项和
项和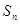 满足
满足 且
且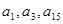 成等比数列,求
成等比数列,求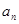 .
. 中,
中, .
. ,求数列
,求数列 的通项公式;
的通项公式; 求证:
求证: .
. 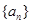 的前
的前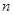 项和为
项和为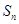 ,点
,点 在直线
在直线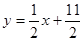 上.数列
上.数列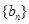 满足
满足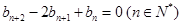 ,且
,且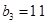 ,前9项和为153.
,前9项和为153.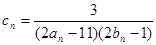 ,数列
,数列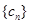 的前
的前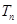 ,求使不等式
,求使不等式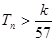 对一切
对一切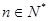 都成立的最大正整数
都成立的最大正整数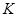 的值;
的值;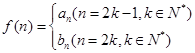 ,问是否存在
,问是否存在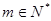 ,使得
,使得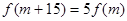 成立?若存在,求出
成立?若存在,求出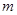 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.