题目内容
已知数列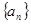 的前
的前 项和为
项和为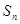
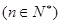 ,设
,设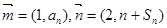 ,且
,且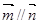 .
.
(1)证明{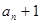 }是等比数列;
}是等比数列;
(2)求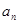 与
与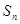 .
.
(1)根据题意 ,结合向量的共线可知,由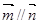 得:
得: 则
则 。两式作差来得到求解。
。两式作差来得到求解。
(2) ,
,
解析试题分析:解:(1)由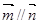 得:
得: 则
则 ,两式相减得
,两式相减得 ,故
,故 ,所以数列
,所以数列 是等比数列
是等比数列
(2)由 令
令 解得
解得 ,所以
,所以 ,即
,即

考点:等比数列
点评:本试题考查了等比数列的定义以及数列的通项公式与前n项和的关系的运用,属于基础题。

练习册系列答案
相关题目
题目内容
已知数列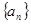 的前
的前 项和为
项和为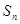
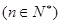 ,设
,设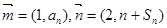 ,且
,且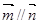 .
.
(1)证明{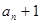 }是等比数列;
}是等比数列;
(2)求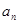 与
与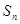 .
.
(1)根据题意 ,结合向量的共线可知,由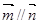 得:
得: 则
则 。两式作差来得到求解。
。两式作差来得到求解。
(2) ,
,
解析试题分析:解:(1)由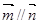 得:
得: 则
则 ,两式相减得
,两式相减得 ,故
,故 ,所以数列
,所以数列 是等比数列
是等比数列
(2)由 令
令 解得
解得 ,所以
,所以 ,即
,即

考点:等比数列
点评:本试题考查了等比数列的定义以及数列的通项公式与前n项和的关系的运用,属于基础题。
