题目内容
16.已知点A,B是圆O:x2+y2=36上的动点,函数y=loga(x-3)(a>0且a≠1)的图象恒过点P,若|$\overrightarrow{PA}$$+\overrightarrow{PB}$|=|$\overrightarrow{PA}$-$\overrightarrow{PB}$|,则平行四边形APBQ的顶点Q的轨迹方程为( )| A. | x2-y2=1 | B. | x2+y2=56 | C. | x2+$\frac{{y}^{2}}{3}$=1 | D. | y2=4x |
分析 设出AB的中点R的坐标、Q的坐标,根据矩形的性质得|AR|=|PR|,利用两点间的距离公式列出方程,再由R是PQ的中点,利用中点坐标公式建立Q、R两点坐标的关系,代入方程化简即可.
解答 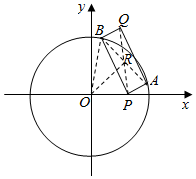 解:如图示:
解:如图示:
函数y=loga(x-3)(a>0且a≠1)的图象横过点P,则P(4,0),
设AB的中点为R,则R也是PQ的中点,设R的坐标为(x1,y1),
若|$\overrightarrow{PA}$$+\overrightarrow{PB}$|=|$\overrightarrow{PA}$-$\overrightarrow{PB}$|,则∠APB=90°,
因为R是弦AB的中点,所以依垂径定理:在Rt△OAR中,|AR|2=|AO|2-|OR|2=36-(${{x}_{1}}^{2}$+${{y}_{1}}^{2}$),
因为∠APB=90°,所以|AR|=|PR|=${{(x}_{1}-4)}^{2}$+${{y}_{1}}^{2}$,
所以(x1-4)2+${{y}_{1}}^{2}$=36-(${{x}_{1}}^{2}$+${{y}_{1}}^{2}$),化简得${{x}_{1}}^{2}$+${{y}_{1}}^{2}$-4x1-10=0,
设Q(x,y),因为R是PQ的中点,所以 $\left\{\begin{array}{l}{{x}_{1}=\frac{x+4}{2}}\\{{y}_{1}=\frac{y}{2}}\end{array}\right.$,
代入上式得,($\frac{x+4}{2}$)2+${(\frac{y}{4})}^{2}$-4×$\frac{x+4}{2}$-10=0,化简得x2+y2=56,
所求的Q点的轨迹方程是x2+y2=56,
故选:B.
点评 本题主要考查利用“相关点代入法”求曲线的轨迹方程,利用平面几何的基本知识和两点间的距离公式建立线段AB中点R的轨迹方程.欲求Q的轨迹方程,应先求R的轨迹方程,若学生思考不深刻,发现不了问题的实质,很难解决此题,属于难题.
