题目内容
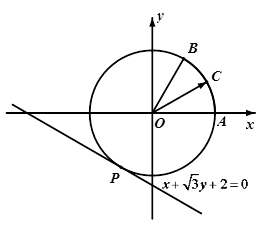
如图,圆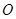 与直线
与直线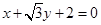 相切于点
相切于点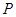 ,与
,与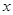 正半轴交于点
正半轴交于点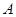 ,与直线
,与直线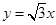 在第一象限的交点为
在第一象限的交点为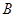 .点
.点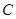 为圆
为圆 上任一点,且满足
上任一点,且满足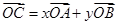 ,动点
,动点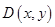 的轨迹记为曲线
的轨迹记为曲线 .
.
(1)求圆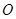 的方程及曲线
的方程及曲线 的方程;
的方程;
(2)若两条直线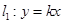 和
和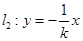 分别交曲线
分别交曲线 于点
于点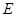 、
、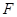 和
和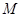 、
、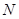 ,求四边形
,求四边形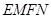 面积的最大值,并求此时的
面积的最大值,并求此时的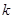 的值.
的值.
(3)证明:曲线 为椭圆,并求椭圆
为椭圆,并求椭圆 的焦点坐标.
的焦点坐标.
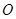 与直线
与直线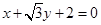 相切于点
相切于点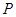 ,与
,与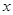 正半轴交于点
正半轴交于点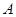 ,与直线
,与直线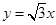 在第一象限的交点为
在第一象限的交点为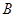 .点
.点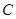 为圆
为圆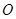 上任一点,且满足
上任一点,且满足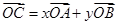 ,动点
,动点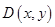 的轨迹记为曲线
的轨迹记为曲线 .
.
(1)求圆
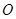 的方程及曲线
的方程及曲线 的方程;
的方程;(2)若两条直线
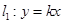 和
和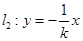 分别交曲线
分别交曲线 于点
于点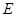 、
、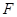 和
和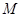 、
、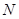 ,求四边形
,求四边形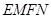 面积的最大值,并求此时的
面积的最大值,并求此时的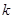 的值.
的值.(3)证明:曲线
 为椭圆,并求椭圆
为椭圆,并求椭圆 的焦点坐标.
的焦点坐标.(1)圆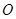 的方程为
的方程为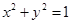 ,曲线
,曲线 的方程为
的方程为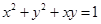 (
(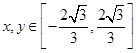 );(2)当
);(2)当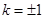 时,四边形
时,四边形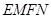 的面积最大值为
的面积最大值为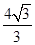 ;(3)证明见解析,其焦点坐标为
;(3)证明见解析,其焦点坐标为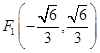 ,
,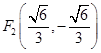 .
.
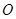 的方程为
的方程为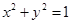 ,曲线
,曲线 的方程为
的方程为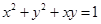 (
(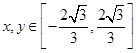 );(2)当
);(2)当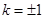 时,四边形
时,四边形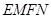 的面积最大值为
的面积最大值为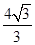 ;(3)证明见解析,其焦点坐标为
;(3)证明见解析,其焦点坐标为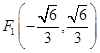 ,
,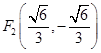 .
.试题分析:(1)圆的半径等于圆心到切线的距离,曲线的方程可通过已知
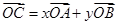 变形得到,条件是
变形得到,条件是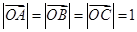 ,
,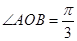 ,把已知式平方可得出
,把已知式平方可得出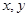 的方程;(2)从
的方程;(2)从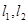 方程可看出
方程可看出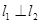 ,即
,即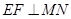 ,因此
,因此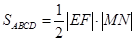 ,我们把
,我们把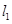 方程与曲线
方程与曲线 方程联立方程组可解得
方程联立方程组可解得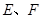 两点坐标,从而得到
两点坐标,从而得到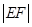 ,把
,把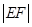 中的
中的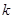 ,用
,用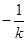 代可得出
代可得出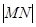 ,从而求出
,从而求出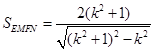 ,变形为
,变形为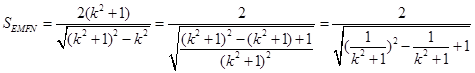
 ,易知
,易知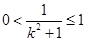 ,故当
,故当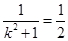 即
即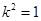 时,
时,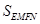 取得最大值
取得最大值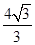 ,为了求最大值,也可作变形
,为了求最大值,也可作变形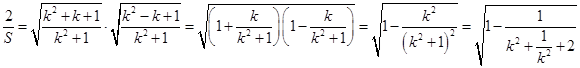 ,应用基本不等式基本不等式知识得出结论;(3)要证曲线
,应用基本不等式基本不等式知识得出结论;(3)要证曲线 为椭圆,首先找它的对称轴,从方程中可看出直线
为椭圆,首先找它的对称轴,从方程中可看出直线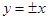 是其对称轴,接着求出曲线与对称轴的交点即椭圆的顶点,这样可求得长轴长
是其对称轴,接着求出曲线与对称轴的交点即椭圆的顶点,这样可求得长轴长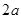 和短轴长
和短轴长 ,根据公式
,根据公式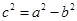 ,求出半焦距
,求出半焦距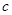 ,这样可求出焦点
,这样可求出焦点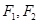 ,下面我们只要按照椭圆的定义证明曲线的点到两定点
,下面我们只要按照椭圆的定义证明曲线的点到两定点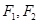 的距离之和为定值
的距离之和为定值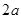 ,也可求出到两定点
,也可求出到两定点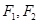 的距离之和为定值
的距离之和为定值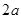 的点的轨迹方程是曲线的方程,这样就完成了证明.
的点的轨迹方程是曲线的方程,这样就完成了证明. 试题解析:(1)由题意圆
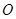 的半径
的半径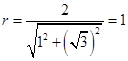 ,
,故圆
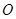 的方程为
的方程为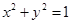 . 2分
. 2分由
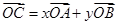 得,
得,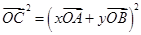 ,
,即
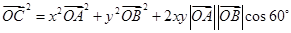 ,得
,得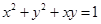 (
(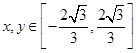 )为曲线
)为曲线 的方程.(未写
的方程.(未写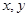 范围不扣分) 4分
范围不扣分) 4分(2)由
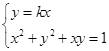 得
得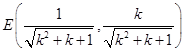 ,
,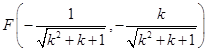 ,
,所以
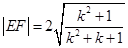 ,同理
,同理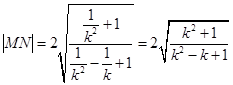 . 6分
. 6分由题意知
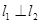 ,所以四边形
,所以四边形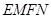 的面积
的面积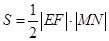 .
.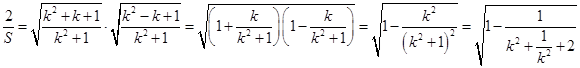 ,
,∵
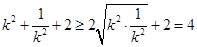 ,∴
,∴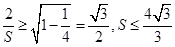 . 8分
. 8分当且仅当
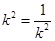 时等号成立,此时
时等号成立,此时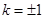 .
.∴ 当
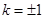 时,四边形
时,四边形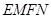 的面积最大值为
的面积最大值为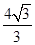 . 10分
. 10分(3)曲线
 的方程为
的方程为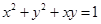 (
(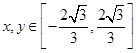 ),它关于直线
),它关于直线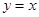 、
、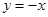 和原点对称,下面证明:
和原点对称,下面证明:设曲线
 上任一点的坐标为
上任一点的坐标为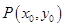 ,则
,则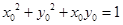 ,点
,点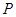 关于直线
关于直线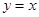 的对称点为
的对称点为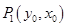 ,显然
,显然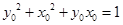 ,所以点
,所以点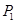 在曲线
在曲线 上,故曲线
上,故曲线 关于直线
关于直线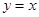 对称,
对称,同理曲线
 关于直线
关于直线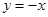 和原点对称.
和原点对称.可以求得
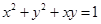 和直线
和直线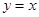 的交点坐标为
的交点坐标为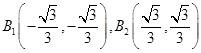
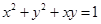 和直线
和直线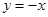 的交点坐标为
的交点坐标为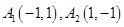 ,
,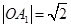 ,
,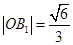 ,
,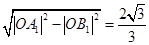 ,
,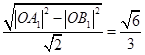 .
.在
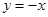 上取点
上取点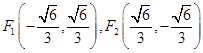
下面证明曲线为椭圆:
ⅰ)设
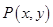 为曲线
为曲线 上任一点,则
上任一点,则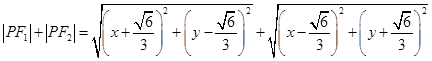
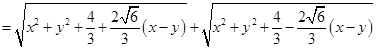
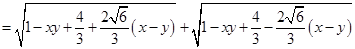
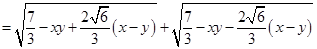
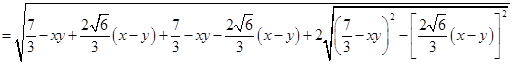
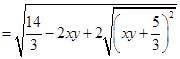
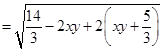 (因为
(因为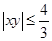 )
)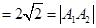 .
.即曲线
 上任一点
上任一点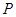 到两定点
到两定点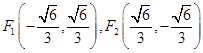 的距离之和为定值
的距离之和为定值 .
.ⅱ)若点
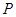 到两定点
到两定点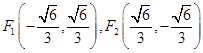 的距离之和为定值
的距离之和为定值 ,可以求得点
,可以求得点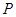 的轨迹方程为
的轨迹方程为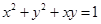 (过程略).
(过程略). 故曲线
 是椭圆,其焦点坐标为
是椭圆,其焦点坐标为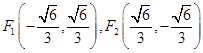 . 18分
. 18分第(3)问说明:
1. ⅰ)、ⅱ)两种情形只需证明一种即可,得5分,
2. 直接写出焦点
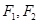 的坐标给3分,未写出理由不扣分.
的坐标给3分,未写出理由不扣分.
练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 到两个定点
到两个定点 、
、 的距离之和为
的距离之和为 ,线段
,线段 的长为
的长为 .
.
 的方程;
的方程;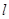 与轨迹
与轨迹 两点,且点
两点,且点 的垂直平分线为
的垂直平分线为 .
. 的面积的最大值;
的面积的最大值; 、
、 关于直线
关于直线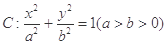 的离心率为
的离心率为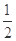 ,以原点
,以原点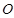 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线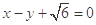 相切。
相切。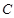 的标准方程;
的标准方程;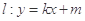 与椭圆
与椭圆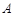 、
、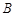 两点,且
两点,且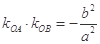 ,试判断
,试判断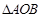 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由. 的离心率为
的离心率为 ,以椭圆的左顶点T为圆心作圆T:
,以椭圆的左顶点T为圆心作圆T: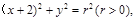 设圆T与椭圆C交于点M、N.
设圆T与椭圆C交于点M、N.
 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程; 轴交于点R,S,O为坐标原点. 试问;是否存在使
轴交于点R,S,O为坐标原点. 试问;是否存在使 最大的点P,若存在求出P点的坐标,若不存在说明理由.
最大的点P,若存在求出P点的坐标,若不存在说明理由. ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 的直线交椭圆
的直线交椭圆 ,
, 两点,
两点,  的距离为
的距离为 ,连接椭圆
,连接椭圆 .
. ,设
,设 是椭圆
是椭圆 两点的直线
两点的直线 交
交 轴于点
轴于点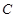 ,若
,若 , 求
, 求 的取值范围;
的取值范围; 与椭圆
与椭圆 ,
, ,其中
,其中 ,若点
,若点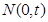 是线段
是线段 垂直平分线上一点,且满足
垂直平分线上一点,且满足 ,求实数
,求实数 的值.
的值. +
+ =1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,
=1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,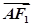 ·
· =0,3|
=0,3| |·|
|·| |=-5
|=-5 ·
· =
= ·
· ?若存在,求出实数m的取值范围;若不存在,说明理由.
?若存在,求出实数m的取值范围;若不存在,说明理由.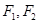 为椭圆C:
为椭圆C: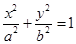
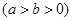 的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率
的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率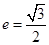 ,
,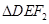 的面积为
的面积为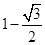 .若点
.若点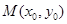 在椭圆C上,则点
在椭圆C上,则点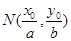 称为点M的一个“椭圆”,直线
称为点M的一个“椭圆”,直线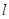 与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.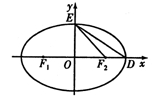
 的直线
的直线 的焦点是双曲线
的焦点是双曲线 的一个焦点,则正数
的一个焦点,则正数 等于( )
等于( )



 (a为长半轴,c为半焦距)上.
(a为长半轴,c为半焦距)上.