题目内容
已知椭圆C: +
+ =1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,
=1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,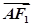 ·
· =0,3|
=0,3| |·|
|·| |=-5
|=-5 ·
· ,|
,| |=2,过点F2且与坐标轴不垂直的直线交椭圆于P,Q两点.
|=2,过点F2且与坐标轴不垂直的直线交椭圆于P,Q两点.
(1)求椭圆C的方程;
(2)线段OF2(O为坐标原点)上是否存在点M(m,0),使得 ·
· =
= ·
· ?若存在,求出实数m的取值范围;若不存在,说明理由.
?若存在,求出实数m的取值范围;若不存在,说明理由.
 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,
=1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,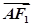 ·
· =0,3|
=0,3| |·|
|·| |=-5
|=-5 ·
· ,|
,| |=2,过点F2且与坐标轴不垂直的直线交椭圆于P,Q两点.
|=2,过点F2且与坐标轴不垂直的直线交椭圆于P,Q两点.(1)求椭圆C的方程;
(2)线段OF2(O为坐标原点)上是否存在点M(m,0),使得
 ·
· =
= ·
· ?若存在,求出实数m的取值范围;若不存在,说明理由.
?若存在,求出实数m的取值范围;若不存在,说明理由.(1)  +
+ =1 (2)存在,其中m∈
=1 (2)存在,其中m∈ .理由见解析
.理由见解析
 +
+ =1 (2)存在,其中m∈
=1 (2)存在,其中m∈ .理由见解析
.理由见解析解:(1)由题意知,∠AF1F2=90°,
cos∠F1AF2=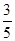 ,
,
注意到| |=2,
|=2,
所以|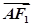 |=
|=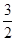 ,|
,| |=
|= ,
,
2a=|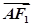 |+|
|+| |=4,
|=4,
所以a=2,c=1,b2=a2-c2=3,
故所求椭圆的方程为 +
+ =1.
=1.
(2)假设存在这样的点M符合题意.
设线段PQ的中点为N,P(x1,y1),Q(x2,y2),N(x0,y0),直线PQ的斜率为k(k≠0),
注意到F2(1,0),则直线PQ的方程为y=k(x-1),
由 得(4k2+3)x2-8k2x+4k2-12=0,
得(4k2+3)x2-8k2x+4k2-12=0,
所以x1+x2= ,
,
故x0= =
= ,
,
又点N在直线PQ上,
所以N .
.
由 ·
· =
= ·
· 可得
可得 ·(
·( +
+ )=2
)=2 ·
· =0,
=0,
即PQ⊥MN,
所以kMN= =-
=- ,
,
整理得m= =
= ∈
∈ ,
,
所以线段OF2上存在点M(m,0)符合题意,
其中m∈ .
.
cos∠F1AF2=
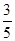 ,
,注意到|
 |=2,
|=2,所以|
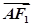 |=
|=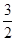 ,|
,| |=
|= ,
,2a=|
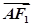 |+|
|+| |=4,
|=4,所以a=2,c=1,b2=a2-c2=3,
故所求椭圆的方程为
 +
+ =1.
=1.(2)假设存在这样的点M符合题意.
设线段PQ的中点为N,P(x1,y1),Q(x2,y2),N(x0,y0),直线PQ的斜率为k(k≠0),
注意到F2(1,0),则直线PQ的方程为y=k(x-1),
由
 得(4k2+3)x2-8k2x+4k2-12=0,
得(4k2+3)x2-8k2x+4k2-12=0,所以x1+x2=
 ,
,故x0=
 =
= ,
,又点N在直线PQ上,
所以N
 .
.由
 ·
· =
= ·
· 可得
可得 ·(
·( +
+ )=2
)=2 ·
· =0,
=0,即PQ⊥MN,
所以kMN=
 =-
=- ,
,整理得m=
 =
= ∈
∈ ,
,所以线段OF2上存在点M(m,0)符合题意,
其中m∈
 .
.
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 与直线
与直线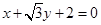 相切于点
相切于点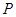 ,与
,与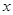 正半轴交于点
正半轴交于点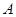 ,与直线
,与直线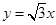 在第一象限的交点为
在第一象限的交点为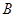 .点
.点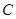 为圆
为圆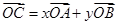 ,动点
,动点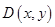 的轨迹记为曲线
的轨迹记为曲线 .
.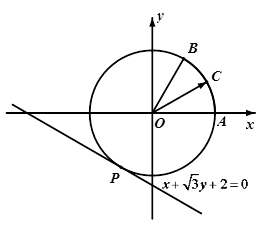
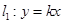 和
和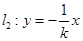 分别交曲线
分别交曲线 、
、 和
和 、
、 ,求四边形
,求四边形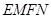 面积的最大值,并求此时的
面积的最大值,并求此时的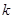 的值.
的值.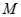 的对称轴为坐标轴,焦点是
的对称轴为坐标轴,焦点是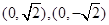 ,又点
,又点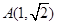 在椭圆
在椭圆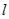 的斜率为
的斜率为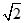 ,若直线
,若直线 、
、 两点,求
两点,求 面积的最大值.
面积的最大值. 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点. 是第一象限内该椭圆上的一点,
是第一象限内该椭圆上的一点, ,求点
,求点 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且
,且 为锐角(其
为锐角(其 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围. 关于直线
关于直线 对称(如图(1)),
对称(如图(1)), ,
, ,将此图形沿
,将此图形沿 折叠成直二面角,连接
折叠成直二面角,连接 、
、 得到几何体(如图(2))
得到几何体(如图(2))
 平面
平面 ;
;  与平面
与平面 的所成角的正切值.
的所成角的正切值. =1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
=1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.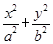 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
. +
+ =t
=t (O为坐标原点),当|
(O为坐标原点),当| -
- |<
|< 时,求实数t的取值范围.
时,求实数t的取值范围. =1(a>b>0)的左焦点为F,短轴端点为B1、B2,
=1(a>b>0)的左焦点为F,短轴端点为B1、B2,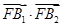 =2b2.
=2b2. 是双曲线
是双曲线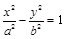 上不同的三点,且
上不同的三点,且 连线经过坐标原点,若直线
连线经过坐标原点,若直线 的斜率乘积
的斜率乘积 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )


