Question

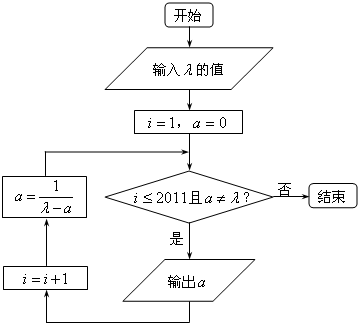（2011•深圳二模）执行下面框图所描述的算法程序，记输出的一列数依次为a₁，a₂，…，a_n，n∈N*，n≤2011．
（1）若输入λ=

2

，写出输出结果；
（2）若输入λ=2，求数列{a_n}的通项公式；
（3）若输入λ＞2，令cn=

an-p

pan-1

，求常数p（p≠±1），使得{c_n}是等比数列．

Answer 1

分析：（1）输入λ=

2

，进行循环得到输出结果是：0，

2

2

．
（2）由题意得an+1=

1

λ-an

，λ=2，所以an+1=

1

2-an

，所以整理得

1

an+1-1

-

1

an-1

=-1（常数），（而{a_n}中的任意一项均不为1）
故{

1

an-1

}是首项为-1，公差为-1的等差数列，可得数列的通项公式．
（3）当λ＞2时，cn+1=p2•

an-p( λ p - 1 p2 )

pan-(pλ-p2)

，令

λ

p

-

1

p2

=1，可得，p=

λ± λ2-4

2

．  所以，pλ-p2=p(p+

1

p

)-p2=1，所以c_n+1=p²c_n，
又c₁=p≠0，故可得答案．

解答：解 （1）输出结果是：0，

2

2

，

2

．
（2）由程序框图知，a₁=0，an+1=

1

λ-an

，n∈N*，n≤2010．
因为λ=2，所以an+1=

1

2-an

，
an+1-1=

1

2-an

-1=

an-1

2-an

，而{a_n}中的任意一项均不为1，
否则的话，由a_n+1=1可以得到a_n=1，…，与a₁=0≠1矛盾，
所以，

1

an+1-1

=

2-an

an-1

=

1

an-1

-1，

1

an+1-1

-

1

an-1

=-1（常数），n∈N*，n≤2010．
故{

1

an-1

}是首项为-1，公差为-1的等差数列，
所以，

1

an-1

=-n，数列{a_n}的通项公式为an=1-

1

n

，n∈N*，n≤2011．
（3）当λ＞2时，cn+1=

an+1-p

pan+1-1

=

1 λ-an -p

p λ-an -1

=

pan-pλ+1

an-λ+p

=p2•

an-p( λ p - 1 p2 )

pan-(pλ-p2)

，
令

λ

p

-

1

p2

=1，则λ=p+

1

p

，p²-λp+1=0，p=

λ± λ2-4

2

．  
此时，pλ-p2=p(p+

1

p

)-p2=1，
所以c_n+1=p²c_n，n∈N*，n≤2011，
又c₁=p≠0，
故存在常数p=

λ± λ2-4

2

（λ＞2），使得{c_n}是以p为首项，p²为公比的等比数列．

点评：本题以框图为桥梁考查数列的有关知识如求数列的通项公式研究判断数列为等比数列，解决此类题目的方法是对求通项公式与判断等比数列的知识要熟悉，要提高运算能力．