题目内容
若曲线f(x)=xsinx+1在x=
处的切线与直线ax+2y+1=0互相垂直,则(ax2-
)5展开式中x的系数为( )
| π |
| 2 |
| 1 |
| x |
| A、40 | B、-10 |
| C、10 | D、-40 |
考点:二项式定理,利用导数研究曲线上某点切线方程
专题:二项式定理
分析:由题意可得 f′(
)=
,求得a=2.在(ax2-
)5=(2x2-
)5 的通项公式中,令x的幂指数等于1,求得r的值,可得(ax2-
)5展开式中x的系数.
| π |
| 2 |
| 2 |
| a |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答:
解:由题意可得曲线f(x)=xsinx+1在x=
处的切线斜率为
,
故有f′(
)=
,即 sin
+
cos
=
,解得a=2.
则(ax2-
)5=(2x2-
)5 的通项公式为 Tr+1=
•25-r•(-1)r•x10-3r,
令10-3r=1,求得r=3,故(ax2-
)5展开式中x的系数为-10×4=-40,
故选:D.
| π |
| 2 |
| 2 |
| a |
故有f′(
| π |
| 2 |
| 2 |
| a |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 2 |
| a |
则(ax2-
| 1 |
| x |
| 1 |
| x |
| C | r 5 |
令10-3r=1,求得r=3,故(ax2-
| 1 |
| x |
故选:D.
点评:本题主要考查导数的几何意义,二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
相关题目
已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中的真命题是( )
| A、若m∥α,n∥β,α∥β,则m∥n |
| B、若m∥α,n∥β,α⊥β,则m⊥n |
| C、若m⊥α,n⊥β,α⊥β,则m∥n |
| D、若m⊥α,n∥β,α∥β,则m⊥n |
已知x,y满足约束条件
,则z=x+3y的最小值为( )
|
| A、1 | B、2 | C、3 | D、4 |
已知函数f(x)=
x3+
ax2+bx+c在x1处取得极大值,在x2处取得最小值,满足x1∈(-1,1),x2∈(2,4),则a+2b的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、(-11,-3) |
| B、(-6,-4) |
| C、(-11,3) |
| D、(-16,-8) |
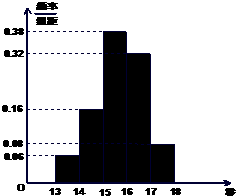 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)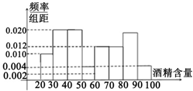 道路安全交通法规定,驾驶员血液酒精含量在20~80mg/100ml,属酒后驾车,血液酒精含量在80mg/100ml以上时,属醉酒驾车,2011年6月1日7:00至22:30,某地查处酒后驾车和醉酒驾车共50起,如图是对这50人的血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数大约为( )
道路安全交通法规定,驾驶员血液酒精含量在20~80mg/100ml,属酒后驾车,血液酒精含量在80mg/100ml以上时,属醉酒驾车,2011年6月1日7:00至22:30,某地查处酒后驾车和醉酒驾车共50起,如图是对这50人的血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数大约为( ) 甲、乙两个学习小组各有10名同学,他们在一次数学测验中成绩的茎叶图(如图),则他们在这次测验中成绩较好的是
甲、乙两个学习小组各有10名同学,他们在一次数学测验中成绩的茎叶图(如图),则他们在这次测验中成绩较好的是