题目内容
设Sn为数列{an}的前n项和,数列{an}满足a1=1,a2=1,且[3+(-1)n]an+2=2an-2[(-1)n-1](n=1,2,3,…). 则S100= .
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件推导出an=
,由此利用分组求和法能求出S100.
|
解答:
解:∵数列{an}满足a1=1,a2=1,且[3+(-1)n]an+2=2an-2[(-1)n-1],
∴n=1时,2a3=2a1+4=6,解得a3=3,
n=2时,4a4=2a2=2,解得a4=
,
n=3时,2a5=2a3+4=10,解得a5=5,
n=4时,4a6=2a4=1,解得a6=
,
当n为奇数时,不妨设n=2m-1,m∈N*,则a2m+1-a2m-1=2.
∴{a2m-1}为等差数列,
∴a2m-1=1+(m-1)•2=2m-1,即an=n
当n为偶数时,设n=2m,m∈N*,则2a2m+2-a2m=0.
∴{a2m}为等比数列,a2m=(
)m-1.
∴an=
,
∴S100=(1+3+5+…+99)+(1+
+
+…+
)
=
(1+99)+
=2500+2-(
)49
=2502-2-49.
故答案为:2502-2-49.
∴n=1时,2a3=2a1+4=6,解得a3=3,
n=2时,4a4=2a2=2,解得a4=
| 1 |
| 2 |
n=3时,2a5=2a3+4=10,解得a5=5,
n=4时,4a6=2a4=1,解得a6=
| 1 |
| 4 |
当n为奇数时,不妨设n=2m-1,m∈N*,则a2m+1-a2m-1=2.
∴{a2m-1}为等差数列,
∴a2m-1=1+(m-1)•2=2m-1,即an=n
当n为偶数时,设n=2m,m∈N*,则2a2m+2-a2m=0.
∴{a2m}为等比数列,a2m=(
| 1 |
| 2 |
∴an=
|
∴S100=(1+3+5+…+99)+(1+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 249 |
=
| 50 |
| 2 |
1×[1-(
| ||
1-
|
=2500+2-(
| 1 |
| 2 |
=2502-2-49.
故答案为:2502-2-49.
点评:本题考查数列的前100项和的求法,推导出an=
,是解题的关键,属于难题.
|

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中的真命题是( )
| A、若m∥α,n∥β,α∥β,则m∥n |
| B、若m∥α,n∥β,α⊥β,则m⊥n |
| C、若m⊥α,n⊥β,α⊥β,则m∥n |
| D、若m⊥α,n∥β,α∥β,则m⊥n |
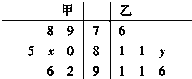 甲、乙两中学各选出7名高一学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲校学生成绩的众数是80,乙校学生成绩的中位数是86,则x+y的值为( )
甲、乙两中学各选出7名高一学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲校学生成绩的众数是80,乙校学生成绩的中位数是86,则x+y的值为( )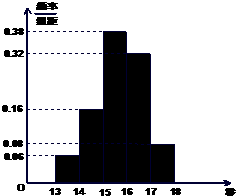 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)