题目内容
19. 某校在2015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…,第六组[130,140],得到如图所示的频率分布直方图.
某校在2015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…,第六组[130,140],得到如图所示的频率分布直方图.(I)求a的值;
(II)这50名学生中成绩在120分以上的同学中任意抽取3人,该3人在130分(含130分)以上的人数记为X,求X的分布列和期望.
分析 (I)根据频率分布直方图频率和为1的性质,能求出成绩在[120,130)的频率.
(II)根据频率分布直方图得X的可能取值为0、1、2、3,分别求出相应的概率,由此能求出X的分布列和期望.
解答 解:(I)根据频率分布直方图,得:
成绩在[120,130)的频率为:
1-(0.01×10+0.024×10+0.03×10+0.016×10+0.008×10)
=1-0.88=0.12…(4分)
(II)根据频率分布直方图得,这50人中成绩在130分以上(包括130分)的有0.08×50=4人,
在[120,140]的学生共有0.12×50+0.08×50=10人…(5分)
所以X的可能取值为0、1、2、3…(6分)
${P}({{X}=0})=\frac{C_6^3}{{C_{10}^3}}=\frac{20}{120}=\frac{1}{6}$,
${P}({{X}=1})=\frac{C_6^2•C_4^1}{{C_{10}^3}}=\frac{60}{120}=\frac{1}{2}$,
${P}({{X}=2})=\frac{C_6^1•C_4^2}{{C_{10}^3}}=\frac{36}{120}=\frac{3}{10}$,
${P}({{X}=3})=\frac{C_4^3}{{C_{10}^3}}=\frac{4}{120}=\frac{1}{30}$…(10分)
所以X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{6}$ | $\frac{1}{2}$ | $\frac{3}{10}$ | $\frac{1}{30}$ |
点评 本题考查频率分在由直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.如图所示的程序框图,它的输出结果是( )


| A. | -1 | B. | 0 | C. | 1 | D. | 16 |
7.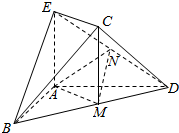 如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
 如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
14.已知数列{bn}中,b1=4,且bn+1-2bn-4=0,则b8=( )
| A. | 28-4 | B. | 210-4 | C. | 212-4 | D. | 29-4 |
8.已知复数$z=\frac{1}{1+i}$,则z的共轭复数$\overline z$等于( )
| A. | $\frac{1}{2}+\frac{i}{2}$ | B. | $\frac{1}{2}-\frac{i}{2}$ | C. | 1+i | D. | 1-i |