题目内容
函数f(x)=sin(x+
)+acos(x+
)的一条对称轴方程为x=
,则实数a等于( )
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
A、2
| ||
B、-
| ||
| C、-2 | ||
D、
|
考点:两角和与差的正弦函数
专题:计算题,三角函数的求值,三角函数的图像与性质
分析:运用两角和的正弦公式化简f(x),得到最值,再由对称轴方程,可得f(
)=±
,代入计算即可求得a.
| π |
| 2 |
| 1+a2 |
解答:
解:函数f(x)=sin(x+
)+acos(x+
)
=
(
sin(x+
)+
cos(x+
))
=
sin(x+
+θ)(θ为辅助角),
由于一条对称轴方程为x=
,
则f(
)=±
,
即为sin(
+
)+acos(
+
)=±
,
即有
-
a=±
,
两边平方,解得,a=-
,
故选B.
| π |
| 3 |
| π |
| 3 |
=
| 1+a2 |
| 1 | ||
|
| π |
| 3 |
| a | ||
|
| π |
| 3 |
=
| 1+a2 |
| π |
| 3 |
由于一条对称轴方程为x=
| π |
| 2 |
则f(
| π |
| 2 |
| 1+a2 |
即为sin(
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 1+a2 |
即有
| 1 |
| 2 |
| ||
| 2 |
| 1+a2 |
两边平方,解得,a=-
| 3 |
故选B.
点评:本题考查三角函数的性质,考查两角和的正弦公式和正弦函数的最值,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式
<0成立的一个充分不必要条件是( )
| 1-x |
| x |
| A、x>1 | B、x<0或x>1 |
| C、0<x<1 | D、x≤0 |
若a<b<0,则下列不等式成立的是( )
| A、ac<bc<0 | ||||
B、
| ||||
C、
| ||||
| D、a2>b2 |
下表中与数x对应的lgx值有且只有一个是错误的,则错误的是( )
| x | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| lgx | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
| A、lg6=1+a-b-c |
| B、lg8=3-3a-3c |
| C、lg12=3-b-2c |
| D、lg27=6a-3b |
已知函数f(x)=2
cosxsin(x+
)-1(x∈R).则函数f(x)在区间[-
,
]上的最大值和最小值分别是( )
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
A、最大值为
| ||||
B、最大值为
| ||||
C、最大值为2
| ||||
| D、最大值为1,最小值为-1 |
在△ABC中,tan
=2sinC,若AB=1,求△ABC周长的取值范围( )
| A+B |
| 2 |
| A、(2,3] |
| B、[1,3] |
| C、(0,2] |
| D、(2,5] |
 如图,某农场要修建3个养鱼塘,每个面积为10000米2,鱼塘前面要留4米的运料通道,其余各边为2米宽的堤埂,则占地面积最少时,每个鱼塘的长、宽分别为( )
如图,某农场要修建3个养鱼塘,每个面积为10000米2,鱼塘前面要留4米的运料通道,其余各边为2米宽的堤埂,则占地面积最少时,每个鱼塘的长、宽分别为( )A、长102米,宽
| ||
| B、长150米,宽66米 | ||
| C、长、宽均为100米 | ||
D、长150米,宽
|
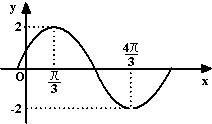 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<