题目内容
14.已知数列{an}的前n项和为Sn,若a1=1,a2n=n-an,a2n+1=an+1,则S100=1306.分析 a2n=n-an,a2n+1=an+1,可得a2n+a2n+1=n+1.由a2n=n-an,a2n+1=an+1,可得a100+a50=50,a50+a25=25,a25=a12+1,a12+a6=6,a6+a3=3,a3=a1+1,a1=1.可得a100.即可得出.
解答 解:∵a2n=n-an,a2n+1=an+1,∴a2n+a2n+1=n+1,
由a2n=n-an,a2n+1=an+1,
可得a100+a50=50,a50+a25=25,a25=a12+1,a12+a6=6,a6+a3=3,a3=a1+1,a1=1.
可得a100=31.
∴S100=a1+(a2+a3)+(a4+a5)+…+(a98+a99)+a100
=1+(1+1)+(2+1)+…+(49+1)+31
=$\frac{50×(1+50)}{2}$+31=1306.
故答案为:1306.
点评 本题考查了数列递推关系、分类讨论方法、分组求和、等差数列的求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
10.已知实数x、y满足$\left\{\begin{array}{l}y≤x-1\\ x≤3\\ x+5y≥4\end{array}\right.$,则$\frac{x^2}{y}$的最小值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.直线l与平面α有无数个公共点,那么1与α的位置关系为( )
| A. | l∥α | B. | l?α | C. | l⊥α | D. | 以上都不对 |
19.甲、乙两人可参加A,B,C三个不同的学习小组,若每人必须参加并且仅能参加一个学习小组,则两人参加同一个学习小组的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
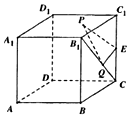 如右图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为$\sqrt{10}$.
如右图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为$\sqrt{10}$.