题目内容
11.设数列{an}中a1=2,an+1=an+2,Sn为{an}的前n项和,若Sn=110,则n=10.分析 利用等差数列的定义、求和公式即可得出.
解答 解:∵数列{an}中a1=2,an+1=an+2,∴数列{an}是等差数列,公差与首项为2.
∴Sn=110=2n+$\frac{n(n-1)}{2}×2$,
化为:n2+n-110=0,n∈N*.
则n=10.
故答案为:10.
点评 本题考查了等差数列的定义、求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.设双曲线$\frac{x^2}{m}+\frac{y^2}{n}=1$的离心率为$\frac{{2\sqrt{3}}}{3}$,且一个焦点与抛物线x2=8y的焦点相同,则此双曲线的方程是( )
| A. | $\frac{y^2}{3}-{x^2}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | C. | ${y^2}-\frac{x^2}{3}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与椭圆$\frac{{x}^{2}}{{m}^{2}}$$+\frac{4{y}^{2}}{{m}^{2}}$=1的离心率互为倒数,则双曲线的渐近线方程是( )
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\frac{1}{3}$x | C. | y=±$\sqrt{3}$x | D. | y=$±\frac{\sqrt{3}}{2}$x |
3.已知函数f(x)=sinωx(ω>0)的最小正周期为π,则下列直线为f(x)的对称轴的是( )
| A. | x=$\frac{π}{2}$ | B. | x=$\frac{π}{3}$ | C. | x=$\frac{π}{4}$ | D. | x=$\frac{π}{5}$ |
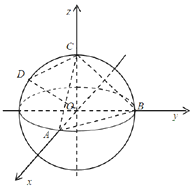 如图所示,球O的球心O在空间直角坐标系O-xyz的原点,半径为1,且球O分别与x,y,z轴的正半轴交于A,B,C三点.已知球面上一点$D({0,-\frac{{\sqrt{3}}}{2},\frac{1}{2}})$.
如图所示,球O的球心O在空间直角坐标系O-xyz的原点,半径为1,且球O分别与x,y,z轴的正半轴交于A,B,C三点.已知球面上一点$D({0,-\frac{{\sqrt{3}}}{2},\frac{1}{2}})$.