题目内容
1.若实数x,y满足不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x≤5}\\{x+2y-11≥0}\end{array}\right.$目标函数z=2x+y的最大值为16.分析 画出约束条件表示的可行域,判断目标函数z=2x+y的位置,求出最大值.
解答  解:作出约束条件不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x≤5}\\{x+2y-11≥0}\end{array}\right.$的可行域如图:
解:作出约束条件不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x≤5}\\{x+2y-11≥0}\end{array}\right.$的可行域如图:
目标函数z=2x+y在$\left\{\begin{array}{l}{x=5}\\{x-y+1=0}\end{array}\right.$的交点A(5,6)处取最大值为z=2×5+6=16.
故答案为:16.
点评 本题考查简单的线性规划的应用,正确画出可行域,判断目标函数经过的位置是解题的关键.

练习册系列答案
相关题目
11.已知函数f(x)=$\left\{\begin{array}{l}{3x+3(x≤-1)}\\{f(x-1)+1(x>-1)}\end{array}\right.$,方程f(x)=x+1的解从小到大排成一个数列{an},该数列的前n项和为Sn,则$\frac{2{S}_{n+3}+10}{n}$的最小值为( )
| A. | $\frac{28}{3}$ | B. | $\frac{19}{2}$ | C. | 6 | D. | 2$\sqrt{10}$+3 |
12.直线x-y-1=0的倾斜角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
13.i为虚数单位,若复数(1+mi)(i+2)是纯虚数,则实数m=( )
| A. | 1 | B. | -1 | C. | $-\frac{1}{2}$ | D. | 2 |
10.过抛物线y2=2px(p>0)的焦点F的直线l,与该抛物线及其准线从上向下依次交于A,B,C三点,若|BC|=3|BF|,且|AF|=3,则该抛物线的标准方程是( )
| A. | y2=2x | B. | y2=3x | C. | y2=4x | D. | y2=6x |
11.在等差数列{an}中,2(a1+a3+a5)+3(a8+a10)=36,则a6=( )
| A. | 8 | B. | 6 | C. | 4 | D. | 3 |
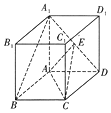 如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上,且E为A1D的中点
如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上,且E为A1D的中点