题目内容
3.设函数f(x)在R上存在导函数f'(x),对任意的实数x都有f(x)=4x2-f(-x),当x∈(-∞,0)时,f'(x)+$\frac{1}{2}$<4x.若f(m+1)≤f(-m)+3m+$\frac{3}{2}$,则实数m的取值范围是( )| A. | $[{-\frac{1}{2},+∞})$ | B. | $[{-\frac{3}{2},+∞})$ | C. | [-1,+∞) | D. | [-2,+∞) |
分析 因为f(x)-2x2+f(-x)-2x2=0,设g(x)=f(x)-2x2,则g(x)+g(-x)=0,可得g(x)为奇函数,又$g'(x)=f'(x)-4x<-\frac{1}{2}$,得g(x)在(-∞,0)上是减函数,从而在R上是减函数,在根据函数的奇偶性和单调性可得g(m+1)≤g(-m),由此即可求出结果.
解答 解:∵f(x)-2x2+f(-x)-2x2=0,
设g(x)=f(x)-2x2+$\frac{1}{2}$x,则g(x)+g(-x)=0,
∴g(x)为奇函数,又g′(x)=f′(x)-4x+$\frac{1}{2}$<0,
∴g(x)在(-∞,0)上是减函数,从而在R上是减函数,
又f(m+1)≤f(-m)+3m+$\frac{3}{2}$,
等价于f(m+1)-2(m+1)2≤f(-m)-2(-m)2,
即g(m+1)≤g(-m),
∴m+1≥-m,解得$m≥-\frac{1}{2}$,
故选:A.
点评 本题考查了函数的单调性、奇偶性问题,考查导数的应用,是一道中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
14.直线a∥平面α,直线b⊥平面α,则直线a与直线b的位置关系为( )
| A. | 异面 | B. | 垂直 | ||
| C. | 平行 | D. | 平行或异面或相交 |
15.函数f(x)=x3-ax+100在区间(1,+∞)内是增函数,则实数a的取值范围是( )
| A. | a<3 | B. | a>3 | C. | a≤3 | D. | a≥3 |
12.点P(x,y)是直线kx+y+3=0上一动点,PA,PB是圆C:x2+y2-4y=0的两条切线,A,B是切点,若四边形PACB面积的最小值为2,则k的值为( )
| A. | $2\sqrt{2}$ | B. | $±2\sqrt{2}$ | C. | 2 | D. | ±2 |
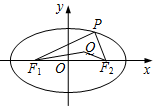 在平面直角坐标系xOy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点分别为F1(-3,0),F2(3,0).点P(x0,y0)是椭圆C在x轴上方的动点,且△PF1F2的周长为16.
在平面直角坐标系xOy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点分别为F1(-3,0),F2(3,0).点P(x0,y0)是椭圆C在x轴上方的动点,且△PF1F2的周长为16.