题目内容
3.圆台的侧面积为$\frac{16}{3}$πcm2,它的内切球的表面积是4πcm2,则圆台的体积为$\frac{26}{9}$πcm3.分析 设圆台的上底面半径为r,下底面半径为R,由切线长定理得母线长为R+r,
由圆台的侧面面积和内切球表面积求出r和R,高是圆台内切球的直径a,由此求出圆台的体积.
解答 解:设圆台的上底面半径为r,下底面半径为R,则母线长为R+r;
设圆台内切球的半径为a,则4πa2=4π,解得a=1;
又圆台的侧面面积是π•(r+R)2=$\frac{16}{3}$π,
解得r+R=$\frac{4}{3}$$\sqrt{3}$①;
画出圆台的轴截面,如图所示: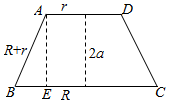
则R-r=$\sqrt{{(R+r)}^{2}{-(2a)}^{2}}$=$\sqrt{\frac{16}{3}-4}$=$\frac{2}{3}$$\sqrt{3}$②,
由①②解得R=$\sqrt{3}$,r=$\frac{1}{3}$$\sqrt{3}$;
∴圆台的体积为V=$\frac{1}{3}$π(r2+rR+R2)h=$\frac{1}{3}$π($\frac{1}{3}$+$\frac{1}{3}$$\sqrt{3}$×$\sqrt{3}$+3)×2=$\frac{26}{9}$π(cm3).
故答案为:$\frac{26}{9}$π.
点评 本题考查了圆台的结构特征与面积、体积的计算问题,根据线切长定理得出母线长为R+r,是简化解题的关键.

练习册系列答案
相关题目
14.等差数列{an}的前n项和为Sn,若$\frac{{S}_{2016}}{2016}$=$\frac{{S}_{2015}}{2015}$+2,则数列{an}的公差为( )
| A. | 2 | B. | 4 | C. | 2015 | D. | 2016 |
8.在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点,己知|AB|=2|OA|,且点B的纵坐标大于0.
(1)求B的坐标;
(2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程.
(1)求B的坐标;
(2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程.
12.在等比数列{an}中,a1+a2=3,a4+a5=24,则a7+a8=( )
| A. | 45 | B. | 171 | C. | 182 | D. | 192 |
13.在y轴上的截距为-2,且与x轴平行的直线的方程为( )
| A. | x=-2 | B. | x+y+2=0 | C. | y=-2 | D. | x-y-2=0 |