题目内容
已知椭圆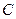 的中心在原点,焦点
的中心在原点,焦点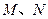 在
在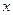 轴上,且焦距为
轴上,且焦距为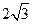 ,实轴长为4
,实轴长为4
(Ⅰ)求椭圆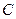 的方程;
的方程;
(Ⅱ)在椭圆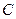 上是否存在一点
上是否存在一点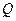 ,使得
,使得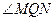 为钝角?若存在,求出点
为钝角?若存在,求出点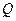 的横坐标的取值范围;若不存在,请说明理由.
的横坐标的取值范围;若不存在,请说明理由.
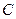 的中心在原点,焦点
的中心在原点,焦点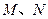 在
在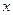 轴上,且焦距为
轴上,且焦距为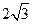 ,实轴长为4
,实轴长为4(Ⅰ)求椭圆
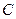 的方程;
的方程; (Ⅱ)在椭圆
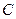 上是否存在一点
上是否存在一点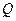 ,使得
,使得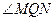 为钝角?若存在,求出点
为钝角?若存在,求出点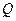 的横坐标的取值范围;若不存在,请说明理由.
的横坐标的取值范围;若不存在,请说明理由.(Ⅰ)设椭圆方程为: ,依题意得:a =" 2" ,c =
,依题意得:a =" 2" ,c =  ,所以b = 1
,所以b = 1
所以椭圆方程为 ……………5分
……………5分
(Ⅱ)假设存在,设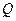 (x,y).则因为
(x,y).则因为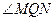 为钝角,所以
为钝角,所以
 ,
, ,
,
又因为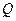 点在椭圆上,所以
点在椭圆上,所以
联立两式得: 化简得:
化简得: ,
,
解得: ,所以存在。
,所以存在。
 ,依题意得:a =" 2" ,c =
,依题意得:a =" 2" ,c =  ,所以b = 1
,所以b = 1所以椭圆方程为
 ……………5分
……………5分(Ⅱ)假设存在,设
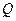 (x,y).则因为
(x,y).则因为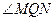 为钝角,所以
为钝角,所以
 ,
, ,
,
又因为
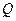 点在椭圆上,所以
点在椭圆上,所以
联立两式得:
 化简得:
化简得: ,
,解得:
 ,所以存在。
,所以存在。略

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
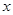 轴上,离心率为
轴上,离心率为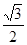 ,且经过点
,且经过点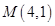 ,直线
,直线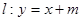 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B.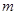 的取值范围。
的取值范围。 、
、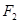 是椭圆
是椭圆 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足 为坐标原点),
为坐标原点), ,若椭圆的离心率等于
,若椭圆的离心率等于
 的面积等于
的面积等于 ,求椭圆的方程;
,求椭圆的方程; 的面积等于
的面积等于 ?若存在,求出点M的坐标;若不存在,说明理由.
?若存在,求出点M的坐标;若不存在,说明理由.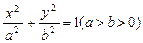 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆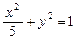 的“左特征点”M的坐标;
的“左特征点”M的坐标;
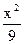 +
+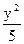 =1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
=1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.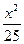 +
+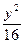 =1上任意一点,F1、F2为左、右焦点,如图所示.
=1上任意一点,F1、F2为左、右焦点,如图所示.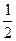 |PF1|;
|PF1|;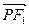 ·
·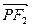 =0,若存在,求出P点的坐标, 若不存在,试说明理由
=0,若存在,求出P点的坐标, 若不存在,试说明理由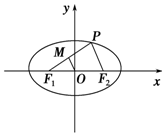
 是椭圆
是椭圆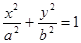
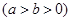 的两个焦点,
的两个焦点,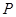 是以
是以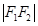 为直径的圆与椭圆的一个交点,且
为直径的圆与椭圆的一个交点,且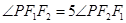 ,则该椭圆的离心率为 ( )
,则该椭圆的离心率为 ( )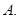 .
.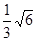
 .
.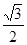
 .
.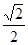
 .
.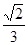
 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为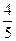 ,且过点
,且过点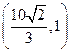 (题干自编)
(题干自编)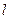 分别切椭圆C与圆
分别切椭圆C与圆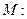
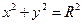 (其中
(其中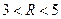 )于
)于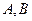 两点,求
两点,求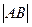 的最大值。
的最大值。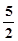 ,一个等比中项是
,一个等比中项是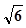 ,且
,且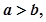 则椭圆
则椭圆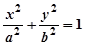 的离心率e等于( )
的离心率e等于( )


