题目内容
P为椭圆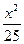 +
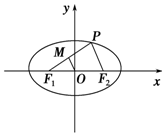
+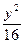 =1上任意一点,F1、F2为左、右焦点,如图所示.
=1上任意一点,F1、F2为左、右焦点,如图所示.
(1)若PF1的中点为M,求证:|MO|=5-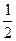 |PF1|;
|PF1|;
(2)若∠F1PF2=60°,求|PF1|·|PF2|之值;
(3)椭圆上是否存在点P,使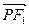 ·
·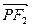 =0,若存在,求出P点的坐标, 若不存在,试说明理由
=0,若存在,求出P点的坐标, 若不存在,试说明理由
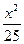 +
+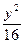 =1上任意一点,F1、F2为左、右焦点,如图所示.
=1上任意一点,F1、F2为左、右焦点,如图所示.(1)若PF1的中点为M,求证:|MO|=5-
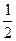 |PF1|;
|PF1|;(2)若∠F1PF2=60°,求|PF1|·|PF2|之值;
(3)椭圆上是否存在点P,使
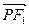 ·
·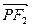 =0,若存在,求出P点的坐标, 若不存在,试说明理由
=0,若存在,求出P点的坐标, 若不存在,试说明理由
(1)证明:在△F1PF2中,MO为中位线,
∴|MO|= =
=
=a- =5-
=5-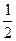 |PF1|.
|PF1|.
(2)解:∵ |PF1|+|PF2|=10,
∴|PF1|2+|PF2|2=100-2|PF1|·|PF2|,
在△PF1F2中,cos 60°= ,
,
∴|PF1|·|PF2|=100-2|PF1|·|PF2|-36,
∴|PF1|·|PF2|= .
.
(3)解:设点P(x0,y0),则 +
+ =1.①
=1.①
易知F1(-3,0),F2(3,0),故PF1=(-3-x0,-y0),
PF2=(-3-x0,-y0),
∵PF1·PF2=0,∴ -9+
-9+ =0,②
=0,②
由①②组成方程组,此方程组无解,故这样的点P不存在.
∴|MO|=
 =
=
=a-
 =5-
=5-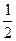 |PF1|.
|PF1|.(2)解:∵ |PF1|+|PF2|=10,
∴|PF1|2+|PF2|2=100-2|PF1|·|PF2|,
在△PF1F2中,cos 60°=
 ,
,∴|PF1|·|PF2|=100-2|PF1|·|PF2|-36,
∴|PF1|·|PF2|=
 .
.(3)解:设点P(x0,y0),则
 +
+ =1.①
=1.①易知F1(-3,0),F2(3,0),故PF1=(-3-x0,-y0),
PF2=(-3-x0,-y0),
∵PF1·PF2=0,∴
 -9+
-9+ =0,②
=0,②由①②组成方程组,此方程组无解,故这样的点P不存在.
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
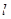 :y=kx+1(k≠0),椭圆E:
:y=kx+1(k≠0),椭圆E: ,若直线
,若直线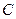 的中心在原点,焦点
的中心在原点,焦点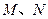 在
在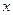 轴上,且焦距为
轴上,且焦距为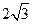 ,实轴长为4
,实轴长为4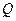 ,使得
,使得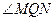 为钝角?若存在,求出点
为钝角?若存在,求出点 、
、 是椭圆
是椭圆 (
( )的两个焦点,
)的两个焦点,  是椭圆上任意一点,从任一焦点引
是椭圆上任意一点,从任一焦点引 的外角平分线的垂线,垂足为
的外角平分线的垂线,垂足为 , 则点
, 则点 . 圆
. 圆  . 椭圆
. 椭圆  . 双曲线
. 双曲线  . 抛物线
. 抛物线 满分12分)已知
满分12分)已知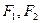 是椭圆
是椭圆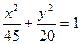 的两个焦点,
的两个焦点,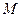 是椭圆上的点,且
是椭圆上的点,且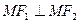 .
.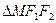 的周长;
的周长;  过点P
过点P ,且离心率为
,且离心率为 ,F为椭圆的右焦点,
,F为椭圆的右焦点, 、
、 两点在椭圆
两点在椭圆 上,且
上,且  ,定点
,定点 (-4,0).
(-4,0).
 时 ,问:MN与AF是否垂直;并证明你的结论.
时 ,问:MN与AF是否垂直;并证明你的结论. =6
=6 时
时 , 求直线MN的方程.
, 求直线MN的方程. 离心率
离心率 ,焦点到椭圆上
,焦点到椭圆上 。
。 与椭圆交与M,N两点,当
与椭圆交与M,N两点,当 时,求直线
时,求直线 的方程。
的方程。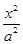 +
+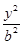 =1(a>b>0)经过点A
=1(a>b>0)经过点A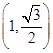 ,且离心率e=
,且离心率e=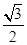 .
. O.若存在,求出直线l的方程;若不存在,说明理由.
O.若存在,求出直线l的方程;若不存在,说明理由. 是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有
是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有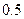 米的距离,现有一货车,车宽
米的距离,现有一货车,车宽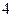 米,车高
米,车高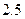 米.
米. 米,则应如何设计隧道才能保证此货车正常通行?
米,则应如何设计隧道才能保证此货车正常通行? 的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?