题目内容
( 9分) 如图,过椭圆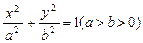 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆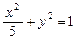 的“左特征点”M的坐标;
的“左特征点”M的坐标;
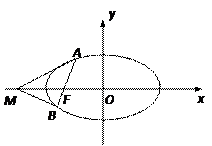
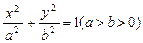 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.求椭圆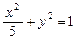 的“左特征点”M的坐标;
的“左特征点”M的坐标;
(1)解:设M(m,0)为椭圆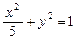 的左特征点,
的左特征点,
椭圆的左焦点为 ,设直线AB的方程为
,设直线AB的方程为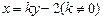
将它代入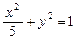 得:
得: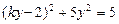 ,
,
即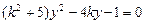
设A(x1,y1),B(x2,y2),则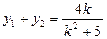 ,
,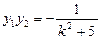
∵∠AMB被x轴平分,∴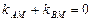
即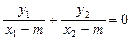 ,Þ
,Þ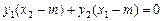
Þ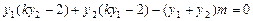
∴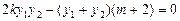 , 于是
, 于是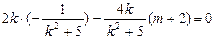
∵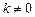 ,∴
,∴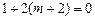 ,即
,即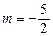 ∴M(
∴M(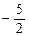 ,0)
,0)
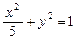 的左特征点,
的左特征点,椭圆的左焦点为
 ,设直线AB的方程为
,设直线AB的方程为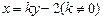
将它代入
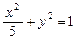 得:
得: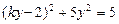 ,
,即
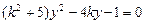
设A(x1,y1),B(x2,y2),则
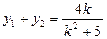 ,
,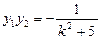
∵∠AMB被x轴平分,∴
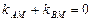
即
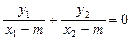 ,Þ
,Þ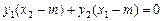
Þ
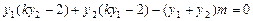
∴
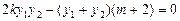 , 于是
, 于是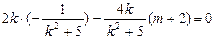
∵
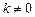 ,∴
,∴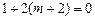 ,即
,即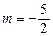 ∴M(
∴M(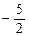 ,0)
,0) 略

练习册系列答案
相关题目
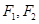 分别为椭圆
分别为椭圆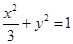 的左、右焦点,点
的左、右焦点,点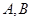 在椭圆上,若
在椭圆上,若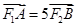 ;则点
;则点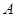 的坐标是 ______.
的坐标是 ______.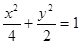 的左右焦点分别为
的左右焦点分别为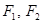 ,过
,过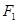 且倾角为
且倾角为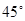 的直线
的直线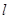 交椭圆于
交椭圆于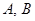 两点,对以下结论:①
两点,对以下结论:①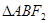 的周长为
的周长为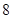 ;②原点到
;②原点到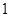 ;③
;③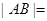
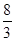 ;其中正确的结论有几个
;其中正确的结论有几个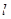 :y=kx+1(k≠0),椭圆E:
:y=kx+1(k≠0),椭圆E: ,若直线
,若直线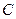 的中心在原点,焦点
的中心在原点,焦点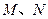 在
在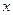 轴上,且焦距为
轴上,且焦距为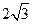 ,实轴长为4
,实轴长为4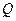 ,使得
,使得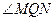 为钝角?若存在,求出点
为钝角?若存在,求出点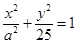 (
(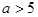 ),它的焦点分别为
),它的焦点分别为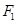 ,
,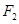 且︱
且︱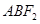 的周长为 ( )
的周长为 ( )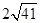 D
D 
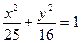 上不同的两点,点C(-3,0),若A、B、C共线,则
上不同的两点,点C(-3,0),若A、B、C共线,则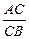 的取值范围是 ▲ .
的取值范围是 ▲ . 是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有
是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有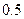 米的距离,现有一货车,车宽
米的距离,现有一货车,车宽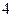 米,车高
米,车高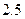 米.
米.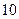 米,则应如何设计隧道才能保证此货车正常通行?
米,则应如何设计隧道才能保证此货车正常通行? 的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
 的左准为准线的抛物线交椭圆C的右准
的左准为准线的抛物线交椭圆C的右准