题目内容
(本题10分)已知椭圆的中心在原点,焦点在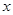 轴上,离心率为
轴上,离心率为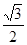 ,且经过点
,且经过点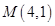 ,直线
,直线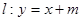 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B.
(1)求椭圆的方程;
(2)求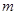 的取值范围。
的取值范围。
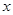 轴上,离心率为
轴上,离心率为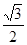 ,且经过点
,且经过点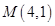 ,直线
,直线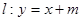 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B.(1)求椭圆的方程;
(2)求
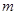 的取值范围。
的取值范围。解:(Ⅰ) , 依题意设椭圆方程为:
, 依题意设椭圆方程为: 把点
把点 代入,得
代入,得
 椭圆方程为
椭圆方程为 (5分)
(5分)
(Ⅱ)把 代入椭圆方程得:
代入椭圆方程得: ,
,
由△ 可得
可得 (10分)
(10分)
 , 依题意设椭圆方程为:
, 依题意设椭圆方程为: 把点
把点 代入,得
代入,得
 椭圆方程为
椭圆方程为 (5分)
(5分)(Ⅱ)把
 代入椭圆方程得:
代入椭圆方程得: ,
,由△
 可得
可得 (10分)
(10分)略

练习册系列答案
相关题目
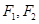 分别为椭圆
分别为椭圆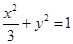 的左、右焦点,点
的左、右焦点,点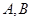 在椭圆上,若
在椭圆上,若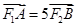 ;则点
;则点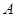 的坐标是 ______.
的坐标是 ______.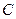 的中心在原点,焦点
的中心在原点,焦点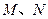 在
在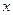 轴上,且焦距为
轴上,且焦距为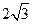 ,实轴长为4
,实轴长为4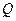 ,使得
,使得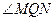 为钝角?若存在,求出点
为钝角?若存在,求出点 的离心率为( )
的离心率为( )

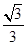

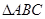 的顶点B,C在椭圆
的顶点B,C在椭圆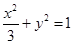 上,顶点A是椭圆的一个焦点,且椭圆的另一个焦点在BC边上,则
上,顶点A是椭圆的一个焦点,且椭圆的另一个焦点在BC边上,则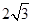
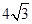
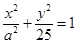 (
(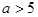 ),它的焦点分别为
),它的焦点分别为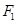 ,
,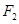 且︱
且︱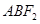 的周长为 ( )
的周长为 ( )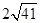 D
D 
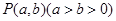 与椭圆
与椭圆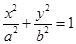 的两个焦点
的两个焦点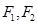 构成等腰三角形,则椭圆的离心率e= ▲
构成等腰三角形,则椭圆的离心率e= ▲  为圆
为圆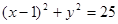 的弦
的弦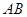 的中点,则直线
的中点,则直线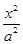 +
+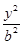 =1(a>b>0)经过点A
=1(a>b>0)经过点A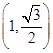 ,且离心率e=
,且离心率e=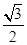 .
. O.若存在,求出直线l的方程;若不存在,说明理由.
O.若存在,求出直线l的方程;若不存在,说明理由.