题目内容
16.已知函数f(x)=sin(2x-$\frac{3π}{4}$)
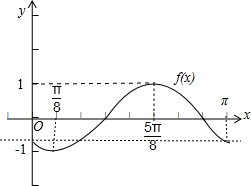
(1)画出函数f(x)在区间[0,π]的简图(要求列表);
(2)求函数f(x)的单调递减区间.
分析 (1)利用用五点法做函数y=Asin(ωx+φ)的图象的方法,作出f(x)在区间[0,π]的简图.
(2)利用正弦函数的减区间,求得函数f(x)的单调递减区间.
解答 解:(1)对于函数f(x)=sin(2x-$\frac{3π}{4}$),∵x∈[0,π],可得2x-$\frac{3π}{4}$∈[-$\frac{3π}{4}$,$\frac{5π}{4}$],列表如下:
| 2x-$\frac{3π}{4}$ | -$\frac{3π}{4}$ | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | π | $\frac{5π}{4}$ |
| x | 0 | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ | π |
| f(x) | -$\frac{\sqrt{2}}{2}$ | -1 | 0 | 1 | 0 | -$\frac{\sqrt{2}}{2}$ |
(2)令2kπ+$\frac{π}{2}$≤2x-$\frac{3π}{4}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{5π}{8}$≤x≤kπ+$\frac{9π}{8}$,
可得函数f(x)的单调递减区间为[kπ+$\frac{5π}{8}$,kπ+$\frac{9π}{8}$],k∈Z.
点评 本题主要考查用五点法做函数y=Asin(ωx+φ)的图象,正弦函数的减区间,属于基础题.

练习册系列答案
相关题目
7.已知双曲线kx2-2ky2=4的一条准线是y=1,则实数k的值是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | 1 | D. | -1 |
11.sin(-$\frac{13π}{4}$)的值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | -$\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
8.若f'(x0)=2,则$\lim_{△x→0}\frac{{f({x_0})-f({x_0}+△x)}}{△x}$=( )
| A. | -1 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
5.设直线l1的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=1+3t}\end{array}\right.$(t为参数),直线l2的方程为y=3x+4,则l1与l2的距离为( )
| A. | 1 | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{3\sqrt{10}}{5}$ | D. | 2 |