题目内容
已知向量
=(1,-2,4),向量
满足以下三个条件:
①
•
=0;
②|
|=10;
③
与向量
=(1,0,0)垂直;
求向量
.
| y |
| x |
①
| y |
| x |
②|
| x |
③
| x |
| n |
求向量
| x |
考点:空间向量的数量积运算
专题:空间向量及应用
分析:设
=(a,b,c),由于
=(1,-2,4),
•
=0,|
|=10,
与向量
=(1,0,0)垂直;可得
•
=a-2b+4c=0,
=10,
•
=a=0,解出即可.
| x |
| y |
| y |
| x |
| x |
| x |
| n |
| y |
| x |
| a2+b2+c2 |
| x |
| n |
解答:
解:设
=(a,b,c),∵
=(1,-2,4),
•
=0,|
|=10,
与向量
=(1,0,0)垂直;
∴
•
=a-2b+4c=0,
=10,
•
=a=0,
解得a=0,c=2
,b=4
.
或a=0,c=-2
,b=-4
.
∴
=±(0,2
,4
).
| x |
| y |
| y |
| x |
| x |
| x |
| n |
∴
| y |
| x |
| a2+b2+c2 |
| x |
| n |
解得a=0,c=2
| 5 |
| 5 |
或a=0,c=-2
| 5 |
| 5 |
∴
| x |
| 5 |
| 5 |
点评:本题考查了向量垂直与数量积的关系、向量的模的计算公式,属于基础题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
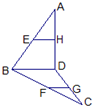 在空间四边形ABCD中,如图所示.
在空间四边形ABCD中,如图所示.