题目内容
1.已知双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的离心率为$\sqrt{2}$,则双曲线的渐近线的夹角为( )| A. | 60° | B. | 45° | C. | 75° | D. | 90° |
分析 利用双曲线的离心率,推出ba的关系,然后求解推出渐近线的夹角.
解答 解:双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的离心率为$\sqrt{2}$,可得a=1,c=$\sqrt{2}$,b=1,
双曲线是等轴双曲线,渐近线y=±x的夹角为90°.
故选:D.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
11.已知复数z满足z(1-i)2=1+i (i为虚数单位),则|z|为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
12.集合A={x|x2-2x<0},B={x|x-2<0},则( )
| A. | A∩B=∅ | B. | A∩B=A | C. | A∪B=A | D. | A∪B=R |
9.将函数$f(x)=sin({2x+φ})({|φ|<\frac{π}{2}})$的图象向左平移$\frac{π}{3}$个单位长度后,所得函数g(x)的图象关于原点对称,则函数f(x)在$[{0,\frac{π}{2}}]$的最大值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
16.已知集合A={1,2,m},B={2,3,4,n},若A∩B={1,2,3},则m-n=( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
11.已知球O的半径为1,A,B是球面上的两点,且AB=$\sqrt{3}$,若点P是球面上任意一点,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围是( )
| A. | [$-\frac{3}{2}$,$\frac{1}{2}$] | B. | [$-\frac{1}{2}$,$\frac{3}{2}$] | C. | [0,$\frac{1}{2}$] | D. | [0,$\frac{3}{2}$] |
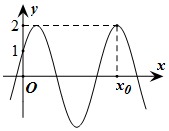 已知函数$f(x)=2sin(2x+φ)(|φ|<\frac{π}{2})$部分图象如图所示.
已知函数$f(x)=2sin(2x+φ)(|φ|<\frac{π}{2})$部分图象如图所示.