题目内容
19.若曲线y=$\sqrt{|{x}^{2}-4|}$与直线y=x+m恰好有两个交点,则实数m的取值范围是(-2,0)∪{2}∪{$2\sqrt{2}$}.分析 把已知曲线方程变形,画出图形,求出双曲线的渐近线方程,再求出直线和圆相切时的m的范围,结合图形即可求得实数m的取值范围.
解答 解:由y=$\sqrt{|{x}^{2}-4|}$,得y2=|x2-4|,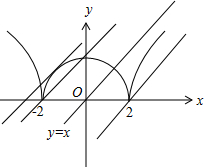
当x2-4≥0时,化为x2-y2=4(y≥0),
当x2-4<0,化为x2+y2=4(y≥0),
图象如图所示,
直线与半圆相切时,m=2$\sqrt{2}$,双曲线的渐近线为y=±x,
∴实数m的取值范围是(-2,0)∪{2}∪{$2\sqrt{2}$}.
故答案为:(-2,0)∪{2}∪{$2\sqrt{2}$}.
点评 本题考查曲线与方程,考查数形结合的数学思想方法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
9.已知函数f(x)=3x+x-5,用二分法求方程3x+x-5=0在x∈(0,2)内近似解的过程中,取区间中点x0=1,那么下一个有根区间为( )
| A. | (0,1) | B. | (1,2) | C. | (1,2)或(0,1)都可以 | D. | 不能确定 |
10.在复平面内,若z=m-3+mi 所对应的点在第二象限,则实数m的取值范围是( )
| A. | (0,3) | B. | (-∞,-2) | C. | (-2,0) | D. | (3,4) |
7.执行如图的程序框图,则输出的S=( )
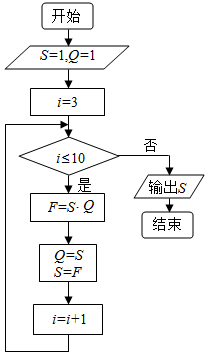

| A. | 21 | B. | 34 | C. | 55 | D. | 89 |
14.执行如图所示的程序框图,若输出的i的值为12,则①、②处可填入的条件分别为( )
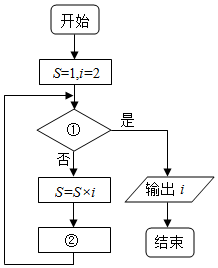

| A. | S>384,i=i+1 | B. | S≥384,i=i+2 | C. | S>3840,i=i+1 | D. | S≥3840,i=i+2 |
9.已知向量$\overrightarrow{m}$≠0,λ∈R,$\overrightarrow{a}$=$\overrightarrow{m}$+λ$\overrightarrow{n}$,$\overrightarrow{b}$=λ$\overrightarrow{n}$,若向量$\overrightarrow{a}$与$\overrightarrow{b}$共线,则( )
| A. | λ=0 | B. | $\overrightarrow{n}$=0 | C. | $\overrightarrow{m}$∥$\overrightarrow{n}$ | D. | λ=0或$\overrightarrow{m}$∥$\overrightarrow{n}$ |
 执行如图的程序框图,那么输出的a是2.
执行如图的程序框图,那么输出的a是2.