题目内容
已知函数f(x)=ax2-2ax+2+b(a≠0),若f(x)在区间[2,3]上有最大值5,最小值2.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)-mx在[2,4]上单调,求m的取值范围.
(1)f(x)=a(x-1)2+2+b-a.
当a>0时,f(x)在[2,3]上为增加的,
 (2)∵b<1,∴a=1,b=0,即f(x)=x2-2x+2,
(2)∵b<1,∴a=1,b=0,即f(x)=x2-2x+2,
g(x)=x2-2x+2-mx=x2-(2+m)x+2,
∵g(x)在[2,4]上单调,
∴ ≥4,∴m≤2或m≥6.
≥4,∴m≤2或m≥6.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 D.y=x|x|
D.y=x|x|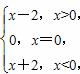 ④f(x)=x2-x-1+lnx中,属于M的有________.(写出所有符合条件的函数序号)
④f(x)=x2-x-1+lnx中,属于M的有________.(写出所有符合条件的函数序号) 等于( )
等于( )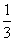 B.
B. C.
C. D.
D.

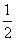 )x的图像之间的关系是( )
)x的图像之间的关系是( )