Question

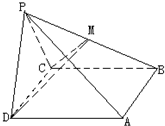（2006•丰台区一模）在四棱锥P-ABCD中，侧面PCD是正三角形，且与底面ABCD垂直，已知底面ABCD是面积为2

3

的菱形，∠ADC=60°，M是PB的中点．
（Ⅰ）求证PA⊥CD；
（Ⅱ）求二面角P-AB-D的度数；
（Ⅲ）求证平面PAB⊥平面CDM．

Answer 1

分析：（Ⅰ）先取CD的中点E，连PE，AE，根据侧面PCD是正三角形，且与底面ABCD垂直可得PE⊥底面ABCD；再结合底面ABCD是面积为2

3

的菱形，∠ADC=60°，即可证PA⊥CD；
（Ⅱ）直接根据CD∥AB，再结合（Ⅰ）所得 AE⊥AB，PA⊥AB可以得到∠PAE是二面角P-AB-D的平面角；再结合菱形的面积求出AB的长，进而求出∠PAE的度数即可；
（Ⅲ）取PA的中点N，连MN，DN，则MN∥AB∥CD，根据AD=PD得到PA⊥ND  结合PA⊥CD即可得PA⊥平面CDM，进而得到平面PAB⊥平面CDM．

解答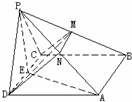：解：（Ⅰ）取CD的中点E，连PE，AE
因为△PCD为正三角形  所以   PE⊥CD
又底面ABCD⊥侧面PCD，因为PE⊥底面ABCD      …（3分）
∠ADC=60°，AD=AC，∴△ADC为正三角形，
所以AE⊥CD    由三垂线定理PA⊥CD   …（5分）
（Ⅱ）因为 CD∥AB，由（Ⅰ）可得 AE⊥AB，PA⊥AB
∴∠PAE是二面角P-AB-D的平面角 …（7分）
因为菱形ABCD是面积S=AB²•sin60°=2

3

，
∴AB=2=CD，PE=AE，∠PAE=45°；
即二面角P-AB-D为45° …（9分）
（Ⅲ）取PA的中点N，连MN，DN，则MN∥AB∥CD
所以 M、N、D、C四点共面，又 因为     AD=PD
∴PA⊥ND  又PA⊥CD
∴PA⊥平面CDM           …（12分）
所以  平面PAB⊥平面CDM                      …（14分）

点评：本题主要考查线线垂直以及面面垂直的证明和二面角的求法．在证明面面垂直时，一般先证明线线垂直，得到线面垂直，进而得到面面垂直．