题目内容
13.直线y=x-$\frac{1}{2}$与抛物线x2=2y的位置关系是相切(填“相交、相切、相离)分析 将直线y=x-$\frac{1}{2}$代入抛物线x2=2y,可得二次方程,求解,即可判断位置关系.
解答 解:将直线y=x-$\frac{1}{2}$代入抛物线x2=2y,
可得x2-2x+1=0,解得x=1,y=$\frac{1}{2}$.
即有直线与抛物线有且只有一个交点,
由直线不平行于对称轴,则直线与抛物线相切.
故答案为:相切.
点评 本题考查直线与抛物线的位置关系的判定,注意联立直线方程和抛物线的方程,由二次方程确定,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.设向量$\overrightarrow{a}$=(cosα,$\frac{1}{2}$),若$\overrightarrow{a}$的模长为$\frac{\sqrt{2}}{2}$,则cos2α等于( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.已知向量$\overrightarrow{m}$=(2x,7),$\overrightarrow{n}$=(6,x+4),若$\overrightarrow{m}$∥$\overrightarrow{n}$且$\overrightarrow{m}$≠$\overrightarrow{n}$,则x的值为( )
| A. | -7或3 | B. | -3或7 | C. | -7 | D. | 3 |
5.如果一个正方体的体积在数值上为v,表面积在数值上为s,且v=s+1,那么这个方体的棱长(精确到0.01)约为( )
| A. | 5.01 | B. | 5.08 | C. | 6.03 | D. | 6.05 |
 已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是32cm3.
已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是32cm3.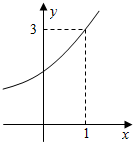 已知函数y=ax+b(b>0)的图象经过点P(1,3),如下图所示,则$\frac{4}{a}+\frac{1}{b}$的最小值为3.
已知函数y=ax+b(b>0)的图象经过点P(1,3),如下图所示,则$\frac{4}{a}+\frac{1}{b}$的最小值为3.