题目内容
已知定点M(0,2),N(-2,0),直线l:kx-y-2k+2=0(k为常数).若点M,N到直线l的距离相等,则实数k的值是 ;对于l上任意一点P,∠MPN恒为锐角,则实数k的取值范围是 .
【答案】分析:由点M(0,2),N(-2,0)到直线l:kx-y-2k+2=0的距离相等,利用点到直线的距离公式求得k的值.
设点P(m,k(m-2)+2),求得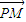 和
和 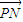 的坐标,由
的坐标,由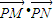 >0恒成立,且
>0恒成立,且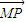 和
和 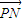 不共线,由此
不共线,由此
解得k的范围.
解答:解:由点M(0,2),N(-2,0)到直线l:kx-y-2k+2=0的距离相等可得
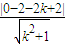 =
=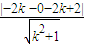 ,解得 k=1,或 k=-
,解得 k=1,或 k=- .
.
直线l:kx-y-2k+2=0 即 y=k(x-2)+2.
设点P(m,k(m-2)+2),则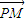 =(-m,2k-km),
=(-m,2k-km),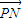 =(-2-m,2k-km-2),
=(-2-m,2k-km-2),
由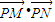 =-m(-2-m)+(2k-km)(2k-km-2)=(1+k2)m2+(2-4k2+2k)m+4k2-4k>0恒成立,
=-m(-2-m)+(2k-km)(2k-km-2)=(1+k2)m2+(2-4k2+2k)m+4k2-4k>0恒成立,
且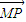 和
和 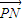 不共线.
不共线.
故有判别式△<0,且-m(2k-km-2)-(2k-km)(-2-m)≠0.
解得 k<- ,或 k>1,
,或 k>1,
故答案为 1或 ;
; 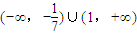 .
.
点评:本题主要考查点到直线的距离公式,两个向量的数量积公式,一元二次不等式的恒成立问题,属于中档题.
设点P(m,k(m-2)+2),求得
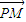 和
和 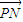 的坐标,由
的坐标,由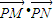 >0恒成立,且
>0恒成立,且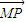 和
和 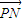 不共线,由此
不共线,由此解得k的范围.
解答:解:由点M(0,2),N(-2,0)到直线l:kx-y-2k+2=0的距离相等可得
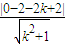 =
=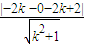 ,解得 k=1,或 k=-
,解得 k=1,或 k=- .
.直线l:kx-y-2k+2=0 即 y=k(x-2)+2.
设点P(m,k(m-2)+2),则
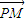 =(-m,2k-km),
=(-m,2k-km),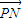 =(-2-m,2k-km-2),
=(-2-m,2k-km-2),由
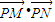 =-m(-2-m)+(2k-km)(2k-km-2)=(1+k2)m2+(2-4k2+2k)m+4k2-4k>0恒成立,
=-m(-2-m)+(2k-km)(2k-km-2)=(1+k2)m2+(2-4k2+2k)m+4k2-4k>0恒成立,且
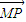 和
和 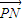 不共线.
不共线.故有判别式△<0,且-m(2k-km-2)-(2k-km)(-2-m)≠0.
解得 k<-
 ,或 k>1,
,或 k>1,故答案为 1或
 ;
; 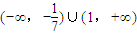 .
.点评:本题主要考查点到直线的距离公式,两个向量的数量积公式,一元二次不等式的恒成立问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目