题目内容
14.直线x+my+3=0与圆x2+y2+x-6y+3=0的交点为P,Q,O为坐标原点,若$\overrightarrow{OP}$⊥$\overrightarrow{OQ}$,求m的值.分析 联立直线和圆的方程,由韦达定理可得y1y2和x1x2,由$\overrightarrow{OP}$⊥$\overrightarrow{OQ}$可得$\overrightarrow{OP}$•$\overrightarrow{OQ}$=x1x2+y1y2=0,解关于m的方程可得.
解答 解:设P(x1,y1),Q(x2,y2),联立直线和圆的方程消去x并整理可得
(1+m2)y2+(5m-6)y+9=0,△=(5m-6)2-36(1+m2)≥0,解得-$\frac{60}{11}$≤m≤0,
由韦达定理可得y1+y2=$\frac{6-5m}{1+{m}^{2}}$,y1y2=$\frac{9}{1+{m}^{2}}$,故x1x2=(-my1-3)(-my2-3)
=m2y1y2+3m(y1+y2)+9=$\frac{3{m}^{2}+18m+9}{1+{m}^{2}}$,
由$\overrightarrow{OP}$⊥$\overrightarrow{OQ}$可得$\overrightarrow{OP}$•$\overrightarrow{OQ}$=x1x2+y1y2=0,化简可得m2+6m+6=0,
解得m=-3+$\sqrt{3}$或m=-3-$\sqrt{3}$,均满足-$\frac{60}{11}$≤m≤0,
故m的值为-3+$\sqrt{3}$或-3-$\sqrt{3}$.
点评 本题考查直线和圆的位置关系,涉及向量的数量积和韦达定理,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.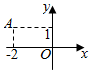 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.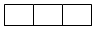 用2种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形中相邻矩形颜色不同的概率是( )
用2种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形中相邻矩形颜色不同的概率是( )
 用2种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形中相邻矩形颜色不同的概率是( )
用2种不同颜色给图中3个矩形随机涂色,每个矩形只涂一种颜色,则3个矩形中相邻矩形颜色不同的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
6.(1+x)4的展开式中x2的系数为( )
| A. | 1 | B. | 4 | C. | 6 | D. | 12 |