题目内容
已知函数f(x)=|x-a|,其中a>1.
(1)当a=2时,求不等式f(x)≥4-|x-4|的解集;
(2)已知关于x的不等式|f(2x+a)-2f(x)|≤2的解集为{x|1≤x≤2},求a的值.
[解析] (1)当a=2时,f(x)+|x-4|
=
当x≤2时,由f(x)≥4-|x-4|得-2x+6≥4,解得x≤1;
当2<x<4时,f(x)≥4-|x-4|无解;
当x≥4时,由f(x)≥4-|x-4|得2x-6≥4,解得x≥5;
所以f(x)≥4-|x-4|的解集为{x|x≤1或x≥5}.
(2)记h(x)=f(2x+a)-2f(x),则
h(x)=
由|h(x)|≤2,解得
又已知|h(x)|≤2的解集为{x|1≤x≤2},
所以 于是a=3.
于是a=3.

练习册系列答案
相关题目
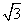 ,BC=3,BE⊥AC,垂足为E,则ED=________.
,BC=3,BE⊥AC,垂足为E,则ED=________.

 +
+ =1的位置关系为( )
=1的位置关系为( )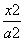 -
-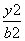 =1(a>0,b>0)的虚轴长为2,焦距为2
=1(a>0,b>0)的虚轴长为2,焦距为2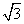 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )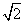 x B.y=±2x
x B.y=±2x x D.y=±
x D.y=± x
x