题目内容
14.如果一个棱柱的底面是正多边形,并且侧棱与底面垂直,这样的棱柱叫做正棱柱,已知一个正六棱柱的各个顶点都在半径为3的球面上,则该正六棱柱的体积的最大值为54.分析 先表示出正六棱柱的体积,再利用导数的方法,即可求出正六棱柱的体积的最大值.
解答 解:设棱柱高为2x(0<x<3),则底面积$S=6×\frac{{\sqrt{3}}}{4}{(\sqrt{9-{x^2}})^2}$,
则$V=Sh=6×\frac{{\sqrt{3}}}{4}{(\sqrt{9-{x^2}})^2}•2x=3\sqrt{3}(9-{x^2})x=-3\sqrt{3}{x^3}+27\sqrt{3}x$
令$V'=-9\sqrt{3}{x^2}+27\sqrt{3}=0解得x=±\sqrt{3}$.
则${V_{max}}=V(\sqrt{3})=-3\sqrt{3}•3\sqrt{3}+27\sqrt{3}•3\sqrt{3}=54$.
故答案为:54.
点评 本题考查正六棱柱的体积的最大值,考查导数知识的运用,正确表示正六棱柱的体积,再利用导数的方法求最大值是关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
3.使|x-4|+|x-3|<a有实数解a的取值范围是( )
| A. | a>7 | B. | 1<a<7 | C. | a>1 | D. | a<7 |
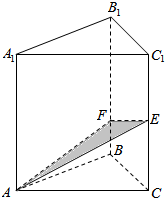 在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形,且∠ABC=90°,E为C1C的中点,点F是BB1上是BF=$\frac{1}{4}$BB1,AC=AA1=2a,求平面EFA与面ABC所成角的大小.
在直三棱柱ABC-A1B1C1中,底面三角形ABC为等腰直角三角形,且∠ABC=90°,E为C1C的中点,点F是BB1上是BF=$\frac{1}{4}$BB1,AC=AA1=2a,求平面EFA与面ABC所成角的大小.