题目内容
16．
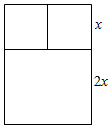一根木料长为42米，要做一个如图的窗框，已知上框架与下框架的高的比为1：2，求：①窗框面积S与x的函数关系式；
②上、下框架的高各为多少时，能使光线通过的窗框面积最大；
③窗框最大面积．
分析 ①求出窗框的高为3x，宽为$\frac{42-7x}{3}$，推出窗框的面积，求出定义域；
②利用二次函数的最值求法，配方，可得最大值时上、下框架的高；
③由②即可得到最大值．
解答 解：①如图设上框高为x，则竖木料总长=3x+4x=7x
三根横木料总长=42-7x，
可得窗框的高为3x，宽为$\frac{42-7x}{3}$，
即窗框的面积为S=3x•$\frac{42-7x}{3}$=-7x2+42x（0＜x＜6）；
②由S=-7x2+42x（0＜x＜6），
配方得，S=-7（x-3）2+63（0＜x＜6）
即有当x=3米时，即上框架高为3米、下框架为6米，
光线通过的窗框面积最大；
③光线通过窗框面积最大为63平方米．
点评 本题考查二次函数在实际问题中的运用，考查函数最值的求法，考查分析问题解决问题的能力，属于中档题．
练习册系列答案
相关题目
6．双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一个焦点F与抛物线C2：y2=2px（p＞0）的焦点相同，它们交于A，B两点，且直线AB过点F，则双曲线C1的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{2}+1$ | D． | 2 |
11．已知实数x，y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{4x-y-4≤0}\end{array}\right.$，则z=3x-y的取值范围为（ ）
| A． | [0，$\frac{12}{5}$] | B． | [0，2] | C． | [2，$\frac{12}{5}$] | D． | [2，$\frac{8}{3}$] |
