题目内容
12.(1)已知$f(x)=(1-3x){(1+x)^5}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_6}{x^6}$,求${a_0}+\frac{1}{3}{a_1}+\frac{1}{3^2}{a_2}+…+\frac{1}{3^6}{a_6}$(2)已知在($\root{3}{x}$-$\frac{1}{2\root{3}{x}}$)n的展开式中,第6项为常数项,求含x2的项的系数;
(3)求和${S_{10}}=C_{10}^1+2C_{10}^2+3C_{10}^3+…+10C_{10}^{10}$.
分析 (1)比较可知求f($\frac{1}{3}$)即可;
(2)利用二项式定理可知展开式中通项公式Tk+1=${C}_{n}^{k}$•${x}^{\frac{n-k}{3}}$•$(-\frac{1}{2\root{3}{x}})^{k}$,利用第6项为常数项可求出n=10,进而可知Tk+1=${C}_{10}^{k}$•$(-\frac{1}{2})^{k}$•${x}^{\frac{10-2k}{3}}$,令$\frac{10-2k}{3}$=2,进而计算即可;
(3)通过倒序相加法,结合二项式定理计算即得结论.
解答 解:(1)∵$f(x)=(1-3x){(1+x)^5}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_6}{x^6}$,
∴${a_0}+\frac{1}{3}{a_1}+\frac{1}{3^2}{a_2}+…+\frac{1}{3^6}{a_6}$=f($\frac{1}{3}$)=(1-3×$\frac{1}{3}$)(1+$\frac{1}{3}$)5=0;
(2)由二项式定理可知($\root{3}{x}$-$\frac{1}{2\root{3}{x}}$)n的展开式中通项公式Tk+1=${C}_{n}^{k}$•${x}^{\frac{n-k}{3}}$•$(-\frac{1}{2\root{3}{x}})^{k}$,
又∵展开式中第6项为常数项,
∴${x}^{\frac{n-5}{3}}$•$(-\frac{1}{2\root{3}{x}})^{5}$为常数,即${x}^{\frac{n-5}{3}}$•${x}^{-\frac{5}{3}}$=1,∴n=10,
∴Tk+1=${C}_{10}^{k}$•${x}^{\frac{10-k}{3}}$•$(-\frac{1}{2})^{k}$•${x}^{-\frac{k}{3}}$=${C}_{10}^{k}$•$(-\frac{1}{2})^{k}$•${x}^{\frac{10-k}{3}}$•${x}^{-\frac{k}{3}}$=${C}_{10}^{k}$•$(-\frac{1}{2})^{k}$•${x}^{\frac{10-2k}{3}}$,
令$\frac{10-2k}{3}$=2,解得:k=2,
∴含x2的项的系数为${C}_{10}^{2}$•$(-\frac{1}{2})^{2}$=$\frac{45}{4}$;
(3)∵${S_{10}}=C_{10}^1+2C_{10}^2+3C_{10}^3+…+10C_{10}^{10}$,
∴S10=${C}_{10}^{9}$+2${C}_{10}^{8}$+…+7${C}_{10}^{3}$+8${C}_{10}^{2}$+9${C}_{10}^{1}$+10${C}_{10}^{0}$,
两式相加,得:2S10=10(${C}_{10}^{10}$+${C}_{10}^{9}$+${C}_{10}^{8}$+…+${C}_{10}^{3}$+${C}_{10}^{2}$+${C}_{10}^{1}$+${C}_{10}^{0}$),
∴S10=5(${C}_{10}^{10}$+${C}_{10}^{9}$+${C}_{10}^{8}$+…+${C}_{10}^{3}$+${C}_{10}^{2}$+${C}_{10}^{1}$+${C}_{10}^{0}$)
=5•(1+1)10
=5•210.
点评 本题考查二项式定理,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | f(1)和f(2) | B. | f(1)和f(-1) | C. | f(-1)和f(2) | D. | f(2)和f(-1) |
| A. | 一个人打靶,打了10发子弹,有7发子弹中靶,因此这个人中靶的概率为0.7 | |
| B. | 一个同学做掷硬币试验,掷了6次,一定有3次“正面朝上” | |
| C. | 某地发行福利彩票,其回报率为47%,有个人花了100元钱买彩票,一定会有47元的回报 | |
| D. | 大量试验后,一个事件发生的频率在0.75附近波动,可以估计这个事件发生的概率为0.75 |
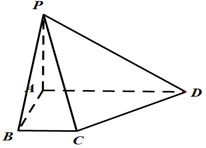 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.