题目内容
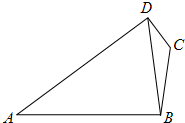
如图，已知四边形ABCD中，AD⊥CD，AD=3，AB=4，∠BDA=60°，∠BCD=135°，求BC的长．
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：在三角形ABD中，利用余弦定理列出关系式，将AD，AB，cos∠BDA的值代入求出BD的长，在三角形BCD中，利用正弦定理即可求出BC的长．
解答：
解：在△ABD中，AD=3，AB=4，∠BDA=60°，
由余弦定理得：AB2=BD2+AD2-2BD•AD•cos∠BDA，即16=BD2+9-3BD，
解得：BD=
（负值舍去），
在△BCD中，
=
，∠BDC=∠ADC-∠ADB=30°，∠BCD=135°，
则BC=
=
=
．
由余弦定理得：AB2=BD2+AD2-2BD•AD•cos∠BDA，即16=BD2+9-3BD，
解得：BD=
3+
| ||
| 2 |
在△BCD中，
| BD |
| sin∠BCD |
| BC |
| sin∠BDC |
则BC=
| BDsin∠BDC |
| sin∠BCD |
| ||||||
|
3
| ||||
| 4 |
点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜
）的最小正周期是π，若其图象向右平移
个单位后得到的函数为奇函数，则函数f（x）的图象（ ）
| π |
| 2 |
| π |
| 6 |
A、关于点（
| ||
B、关于x=
| ||
C、关于点（
| ||
D、关于x=
|