题目内容
如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.
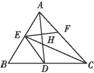
(1)证明:B,D,H,E四点共圆;
(2)证明:CE平分∠DEF.
证明:(1)在△ABC中,∵∠B=60°,
∴∠BAC+∠BCA=120°.
∵AD,CE是角平分线,
∴∠HAC+∠HCA=60°,∴∠AHC=120°.
∴∠EHD=∠AHC=120°.
∵∠EBD+∠EHD=180°,
∴B,D,H,E四点共圆.
(2)如图所示,连结BH,
则BH为∠ABC的平分线,
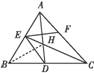
得∠HBD=30°.
由(1)知B,D,H,E四点共圆,
∴∠CED=∠HBD=30°.
又∠AEH=∠EBD=60°,AE=AF,AH平分∠EAF,
∴EF⊥AD.可得∠CEF=30°.
∴CE平分∠DEF.

练习册系列答案
相关题目
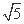 (B)1∶2 (C)1∶
(B)1∶2 (C)1∶ -
-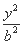 =1(a>0,b>0)的离心率为2,则
=1(a>0,b>0)的离心率为2,则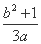 的最小值为( )
的最小值为( )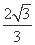 (B)
(B)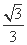 (C)2 (D)1
(C)2 (D)1
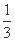 AC,
AC, AB,BD,CE相交于点F.
AB,BD,CE相交于点F.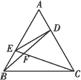
 +
+ ,Q=
,Q= +
+ (a≥0),则P、Q的大小关系是( )
(a≥0),则P、Q的大小关系是( ) ≤f
≤f ,已知函数y=sin x在区间
,已知函数y=sin x在区间 ≤x≤
≤x≤ )的最大值与最小值分别为( )
)的最大值与最小值分别为( ) ,最小值为-
,最小值为-
 -
- =1的离心率为
=1的离心率为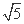 ,则m的值为 .
,则m的值为 .